题目内容
18.张老师决定带领部分学生外出参观,甲旅行社承诺:“如果老师买全票一张,则学生可享受6折优惠”;乙旅行社承诺:“包括老师在内所有人按全票的7折优惠”,全票价为300元.(1)设学生数为x,甲、乙旅行社收费分别为y甲(元)和y乙(元),分别写出两个旅行社收费的表达式;
(2)当学生人数为多少时,两旅行社费用一样;
(3)学生人数为5人时,选择哪家旅行社划算?
分析 (1)根据甲旅行社的收费标准,可得甲的函数解析式;根据乙的收费标准,可得乙的函数解析式;
(2)根据收费相同,可得方程,根据解方程,可得答案;
(3)根据自变量的值,可得相应的函数值,根据有理数的大小比较,可得答案.
解答 解:(1)y甲=300+300×0.6x,即y甲=300+180x;
y乙=300×0.7×(x+1),即y乙=210+210x;
(2)由题意得y甲=y乙,
则:300+180x=210+210x,解之得:x=3
答:当学生人数为3人时,两旅行社费用一样;
(3)当x=5,y甲=300+180×5=1200元;y乙=210+210×5=1260元;
∵1200<1620,
∴选择甲旅行社划算.
点评 本题考查了函数关系式,利用收费标准得出函数关系式是解题关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
9.数轴上点M到1的距离是5,则点M表示的数是( )
| A. | 6 | B. | -4 | C. | 6或-4 | D. | 不能确定 |
6.一只不透明的箱子里共有8个球,其中2个白球,1个红球,5个黄球,它们除颜色外均相同.
(1)从箱子中随机摸出一个球是白球的概率是多少?
(2)再往箱子中放入黄球多少个,可以使摸到白球的概率达到0.2?
(1)从箱子中随机摸出一个球是白球的概率是多少?
(2)再往箱子中放入黄球多少个,可以使摸到白球的概率达到0.2?
13.单项式$-\frac{{πx{y^4}}}{2014}$系数是( )
| A. | -2014 | B. | $-\frac{1}{2014}$ | C. | -π | D. | $-\frac{π}{2014}$ |
10.P是∠B的角平分线和∠C的角平分线在△ABC内的交点,∠BPC=120°,则∠A=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 70° |
8.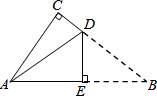 如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
 如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )| A. | 4cm | B. | 5cm | C. | 6cm | D. | 10cm |
 如图,把矩形ABCD沿EF对折,若∠1=60°,则∠AEF等于120°.
如图,把矩形ABCD沿EF对折,若∠1=60°,则∠AEF等于120°.