题目内容
17.已知x1,x2(x1>x2)是方程x2-2x+a=0的两个实数根,且x1+2x2=3-$\sqrt{2}$.(1)求x1,x2及a的值;
(2)求(x1-2)(x2-2)的值.
分析 (1)根据根与系数的关系得到得x1+x2=2,x1x2=a,再利用x1+2x2=3-$\sqrt{2}$,可先计算出x2=1-$\sqrt{2}$,再计算出x1=1+$\sqrt{2}$,最后计算出a的值;
(2)先展开得到原式=x1x2-2(x1+x2)+4,然后利用整体代入的方法计算.
解答 解:(1)根据题意得x1+x2=2,x1x2=a,
∵x1+2x2=3-$\sqrt{2}$,
∴x2=1-$\sqrt{2}$,
∴x1=1+$\sqrt{2}$,
∴a=(1+$\sqrt{2}$)(1-$\sqrt{2}$)=1-2=-1;
(2)原式=x1x2-2(x1+x2)+4=-1-2×2+4=-1.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.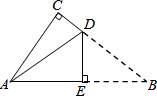 如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
 如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )| A. | 4cm | B. | 5cm | C. | 6cm | D. | 10cm |

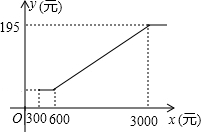 如图所示是我市企业职工养老保险个人月缴费y(元)随个人工资x(元)变化的图象,请你根据图象回答下面的问题:
如图所示是我市企业职工养老保险个人月缴费y(元)随个人工资x(元)变化的图象,请你根据图象回答下面的问题: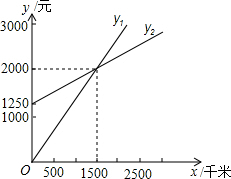 某单位准备租用一辆汽车,设汽车每月行驶x km,甲,乙两个出租车公司的月收费分别为y1元和y2元,y1,y2与x之间的函数关系图象如图,观察图象回答下列问题:
某单位准备租用一辆汽车,设汽车每月行驶x km,甲,乙两个出租车公司的月收费分别为y1元和y2元,y1,y2与x之间的函数关系图象如图,观察图象回答下列问题: