题目内容
19.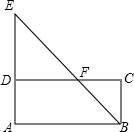 如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )| A. | $\frac{ED}{BC}$=$\frac{EF}{FB}$ | B. | $\frac{DE}{AD}$=$\frac{DF}{AB}$ | C. | $\frac{BC}{DE}$=$\frac{CF}{DF}$ | D. | $\frac{BF}{BE}$=$\frac{BC}{AE}$ |
分析 先根据矩形的性质得AD∥BC,CD∥AB,再根据平行线分线段成比例定理,由DE∥BC得到$\frac{DE}{BC}$=$\frac{EF}{FB}$,$\frac{BC}{DE}$=$\frac{CF}{DF}$,则可对A、C进行判断;由DF∥AB得$\frac{DE}{AE}$=$\frac{DF}{AB}$,则可对B进行判断;由于$\frac{AD}{AE}$=$\frac{BF}{BE}$,利用BC=AD,则可对D进行判断.
解答 解:∵四边形ABCD为矩形,
∴AD∥BC,CD∥AB,
∵DE∥BC,
∴$\frac{DE}{BC}$=$\frac{EF}{FB}$,$\frac{BC}{DE}$=$\frac{CF}{DF}$,所以A、C选项结论正确;
∵DF∥AB,
∴$\frac{DE}{AE}$=$\frac{DF}{AB}$,所以B选项的结论错误;
$\frac{AD}{AE}$=$\frac{BF}{BE}$,
而BC=AD,
∴$\frac{BF}{BE}$=$\frac{BC}{AE}$,所以D选项的结论正确.
故选B.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
10.数轴上A点表示5,B点表示-3,则A与B的距离是( )
| A. | -8 | B. | 8 | C. | 2 | D. | -2 |
8. 已知:如图,∠A=25°,∠CED=95°,∠D=40°,则∠B的度数为( )
已知:如图,∠A=25°,∠CED=95°,∠D=40°,则∠B的度数为( )
 已知:如图,∠A=25°,∠CED=95°,∠D=40°,则∠B的度数为( )
已知:如图,∠A=25°,∠CED=95°,∠D=40°,则∠B的度数为( )| A. | 20° | B. | 160° | C. | 120° | D. | 65° |
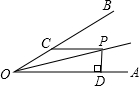 如图,∠AOB=30°,P为∠AOB平分线上一点,PC∥OA交OB于点C,PD⊥OA于点D,若PD+PC=12,则0C的长为8.
如图,∠AOB=30°,P为∠AOB平分线上一点,PC∥OA交OB于点C,PD⊥OA于点D,若PD+PC=12,则0C的长为8.
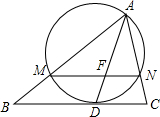 如图,在△ABC中,已知AB=9,BC=8,CA=7,AD为内角平分线,以AD为弦作一圆.该圆与BC相切,与AB交于M,与AC交于N,则BM+CN=4.
如图,在△ABC中,已知AB=9,BC=8,CA=7,AD为内角平分线,以AD为弦作一圆.该圆与BC相切,与AB交于M,与AC交于N,则BM+CN=4.