题目内容
14.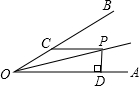 如图,∠AOB=30°,P为∠AOB平分线上一点,PC∥OA交OB于点C,PD⊥OA于点D,若PD+PC=12,则0C的长为8.
如图,∠AOB=30°,P为∠AOB平分线上一点,PC∥OA交OB于点C,PD⊥OA于点D,若PD+PC=12,则0C的长为8.
分析 过点P作PE⊥OA于点E,根据角平分线上的点到角的两边的距离相等可得PE=PD,再根据两直线平行,内错角相等可得∠POD=∠OPC,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠PCE=∠AOB,再根据直角三角形30°角所对的直角边等于斜边的一半解答即可.
解答  解:如图,过点P作PE⊥OA于点E,
解:如图,过点P作PE⊥OA于点E,
∵OP是∠AOB的平分线,
∴PE=PD,
∵PC∥OB,
∴∠POD=∠OPC,
∴∠PCE=∠POC+∠OPC=∠POC+∠POD=∠AOB=30°,
∴PC=2PE=2PD,
∵PD+PC=12,
∴PC=8,
∵∠POD=∠OPC,∠COP=∠DOP,
∴∠COP=∠CPO,
∴OC=PC=8,
故答案为:8.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,以及三角形的一个外角等于与它不相邻的两个内角的和,作辅助线构造含30°角的直角三角形是解题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
2.下列说法正确的是( )
| A. | 面积相等的两个三角形全等 | B. | 周长相等的两个三角形全等 | ||
| C. | 形状相同的两个三角形全等 | D. | 成轴对称的两个三角形全等 |
9.如图所示,下列图案中是轴对称图形的共有( )


| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
19.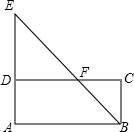 如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
 如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )| A. | $\frac{ED}{BC}$=$\frac{EF}{FB}$ | B. | $\frac{DE}{AD}$=$\frac{DF}{AB}$ | C. | $\frac{BC}{DE}$=$\frac{CF}{DF}$ | D. | $\frac{BF}{BE}$=$\frac{BC}{AE}$ |
6.因为$\frac{3}{4}$a=1,所以( )
| A. | $\frac{3}{4}$是倒数 | B. | a是倒数 | C. | $\frac{3}{4}$和a都是倒数 | D. | $\frac{3}{4}$和a互为倒数 |
 如图所示是由几个小立方块所搭的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,请画出相应几何体的从正面看的图和从左面看的图:
如图所示是由几个小立方块所搭的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,请画出相应几何体的从正面看的图和从左面看的图: