题目内容
在Rt△ABC中,∠B=90°,AC:AB=3:1,求sinC、cosC、tanC.
考点:锐角三角函数的定义,勾股定理
专题:
分析:先由AC:AB=3:1,可设AB=x,则AC=3x,根据勾股定理求出BC=2
x,再根据锐角三角函数的定义即可求解.
| 2 |
解答: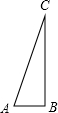 解:∵AC:AB=3:1,
解:∵AC:AB=3:1,
∴可设AB=x,则AC=3x,
根据勾股定理,得BC=
=2
x,
∴sinC=
=
cosC=
=
=
tanC=
=
=
.
 解:∵AC:AB=3:1,
解:∵AC:AB=3:1,∴可设AB=x,则AC=3x,
根据勾股定理,得BC=
| AC2-AB2 |
| 2 |
∴sinC=
| AB |
| AC |
| 1 |
| 3 |
cosC=
| BC |
| AC |
2
| ||
| 3x |
2
| ||
| 3 |
tanC=
| AB |
| BC |
| x | ||
2
|
| ||
| 4 |
点评:本题考查了锐角三角函数的定义,在Rt△ABC中,∠C=90°.
(1)正弦:我们把锐角A的对边a与斜边c的比叫做∠A的正弦,记作sinA.
即sinA=∠A的对边:斜边=a:c.
(2)余弦:锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cosA.
即cosA=∠A的邻边:斜边=b:c.
(3)正切:锐角A的对边a与邻边b的比叫做∠A的正切,记作tanA.
即tanA=∠A的对边:∠A的邻边=a:b.
(4)三角函数:锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
同时考查了勾股定理.
(1)正弦:我们把锐角A的对边a与斜边c的比叫做∠A的正弦,记作sinA.
即sinA=∠A的对边:斜边=a:c.
(2)余弦:锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cosA.
即cosA=∠A的邻边:斜边=b:c.
(3)正切:锐角A的对边a与邻边b的比叫做∠A的正切,记作tanA.
即tanA=∠A的对边:∠A的邻边=a:b.
(4)三角函数:锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
同时考查了勾股定理.

练习册系列答案
相关题目
 如图,直线a与直线c相交于点O,则∠1的度数是( )
如图,直线a与直线c相交于点O,则∠1的度数是( )| A、60° | B、50° |
| C、40° | D、30° |
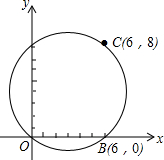 在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由这三个观测点确定的圆形区域是海洋生物保护区.
在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由这三个观测点确定的圆形区域是海洋生物保护区.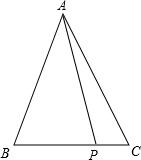 在△ABC中,AB=AC=5cm,P是BC边上一点,证明:无论底边BC的长度是多少,以及点P在BC上的位置如何,PA2+PB•PC的值总是常数.
在△ABC中,AB=AC=5cm,P是BC边上一点,证明:无论底边BC的长度是多少,以及点P在BC上的位置如何,PA2+PB•PC的值总是常数.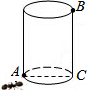 如图,圆柱体蜜桶的半径为1cm,高为3cm,桶内所装蜜的高度距点B为1cm,在点A处有一只蚂蚁,若蚂蚁沿圆柱体的外表面爬行到内表面BC 线的某点处吃蜜,它爬行的最短路线是多少?
如图,圆柱体蜜桶的半径为1cm,高为3cm,桶内所装蜜的高度距点B为1cm,在点A处有一只蚂蚁,若蚂蚁沿圆柱体的外表面爬行到内表面BC 线的某点处吃蜜,它爬行的最短路线是多少? 如图,在△ABC中,∠C=90°∠B=30°,AD是∠BAC的角平分线.若AD=4,求AB的长.
如图,在△ABC中,∠C=90°∠B=30°,AD是∠BAC的角平分线.若AD=4,求AB的长. 如图,∠AOB和∠COD都是直角,OE是OD的反向延长线.
如图,∠AOB和∠COD都是直角,OE是OD的反向延长线.