题目内容
 如图,在△ABC中,∠C=90°∠B=30°,AD是∠BAC的角平分线.若AD=4,求AB的长.
如图,在△ABC中,∠C=90°∠B=30°,AD是∠BAC的角平分线.若AD=4,求AB的长.考点:含30度角的直角三角形,勾股定理
专题:
分析:首先根据角平分线的性质可得∠CAD=∠DAB=
∠CAB=30°,再根据等角对等边可得BD=AD,再根据在直角三角形中,30°角所对的直角边等于斜边的一半可得CD长,进而可得答案.
| 1 |
| 2 |
解答:解:∵∠C=90°∠B=30°,
∴∠CAB=60°,
∵AD是∠BAC的角平分线,
∴∠CAD=∠DAB=
∠CAB=30°,
∴BD=AD=4,CD=
AD,
∴CD=2,
∴BC=6,AC=
=2
,
∴AB=2AC=4
.
∴∠CAB=60°,
∵AD是∠BAC的角平分线,
∴∠CAD=∠DAB=
| 1 |
| 2 |
∴BD=AD=4,CD=
| 1 |
| 2 |
∴CD=2,
∴BC=6,AC=
| AD2-CD2 |
| 3 |
∴AB=2AC=4
| 3 |
点评:此题主要考查了直角三角形的性质,关键是掌握在直角三角形中,30°角所对的直角边等于斜边的一半.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
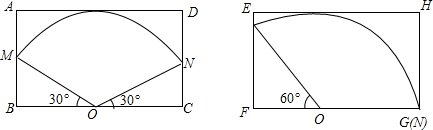
 如图,每个小正方形的边长均为1,求△ABC的三边长.
如图,每个小正方形的边长均为1,求△ABC的三边长.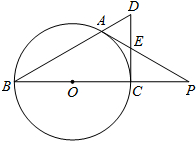 如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D.若CD的中点E,AE的延长线与BC的延长线交于点P.
如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D.若CD的中点E,AE的延长线与BC的延长线交于点P. 已知:如图,C、D为半圆上的两点,且
已知:如图,C、D为半圆上的两点,且