题目内容
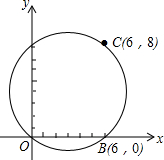 在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由这三个观测点确定的圆形区域是海洋生物保护区.
在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由这三个观测点确定的圆形区域是海洋生物保护区.(1)画出圆形区域的中心位置P,并写出点P的坐标;
(2)若在观测点O测得一艘渔船D的位置为(4,8.5),试问该渔船是否已进入海洋生物保护区?请通过计算回答.
考点:点与圆的位置关系,坐标与图形性质,三角形的外接圆与外心
专题:
分析:(1)连接BC,则点P在OB和BC的垂直平分线上,由条件可知OC为圆的直径,圆心到OB的距离为4,到BC的距离为3,则到y轴的距离为6-3,可得出点P的坐标;
(2)过P作PE⊥OB,交OB于点E,并延长EP交圆于点F,过D作DM⊥EF交EF于点M,连接DP,在Rt△DMP中可求得DP,再比较与半径的大小关系即可得出结论.可判断出P点在圆内,可得出结论.
(2)过P作PE⊥OB,交OB于点E,并延长EP交圆于点F,过D作DM⊥EF交EF于点M,连接DP,在Rt△DMP中可求得DP,再比较与半径的大小关系即可得出结论.可判断出P点在圆内,可得出结论.
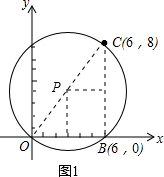
解答:解:(1)由垂径定理可知点P在OB和BC的垂直平分线上,连接BC,如图1,
∵B(6,0),C(6,8),
∴BC⊥OB,
∴OC为直径,
∴点P的坐标为(3,4);
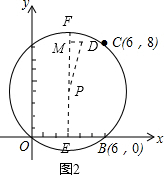
(2)如图2,过P作PE⊥OB,交OB于点E,并延长EP交圆于点F,
过D作DM⊥EF交EF于点M,连接DP,
因为D为(4,8.5),P为(3,4),
所以DM=4-3=1,而MP=8.5-4=4.5,
在Rt△DMP中,由勾股定理可求得DP=
=
=
<
,
即DP<5,
所以点D在⊙P内,所以该渔船已进入海洋生物保护区.
∵B(6,0),C(6,8),
∴BC⊥OB,
∴OC为直径,
∴点P的坐标为(3,4);

(2)如图2,过P作PE⊥OB,交OB于点E,并延长EP交圆于点F,
过D作DM⊥EF交EF于点M,连接DP,
因为D为(4,8.5),P为(3,4),
所以DM=4-3=1,而MP=8.5-4=4.5,
在Rt△DMP中,由勾股定理可求得DP=
| DM2+MP2 |
| 12+4.52 |
| 20.25 |
| 25 |
即DP<5,
所以点D在⊙P内,所以该渔船已进入海洋生物保护区.

点评:本题主要考查点与圆的位置关系及垂径定理的应用,掌握点与圆的位置关系的判定只需要求得点到圆心的距离与半径的大小关系是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若x1,x2是方程x2-6x+8的两根,则x1+x2的值是( )
| A、8 | B、-8 | C、-6 | D、6 |
分式
有意义,则x的取值范围是( )
| 2x |
| x+1 |
| A、x≠1 | B、x≠0 |
| C、x=-1 | D、x≠-1 |
在同学们学习的运算法则中,我们补充定义新运算“%”,它的运算规则是:a%b=(a-b)×(b-a),则3%6=( )
| A、9 | B、18 | C、-9 | D、2 |
 如图有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,绕着中心旋转其中一个正方形,那么图中阴影部分的面积是( )
如图有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,绕着中心旋转其中一个正方形,那么图中阴影部分的面积是( )| A、无法确定 |
| B、8cm2 |
| C、16cm2 |
| D、4cm2 |