题目内容
4.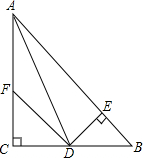 如图所示,在△ABC中,DE⊥AB交AB于E,DE=CD,F在AC上,BD=DF,CF=BE,证明:
如图所示,在△ABC中,DE⊥AB交AB于E,DE=CD,F在AC上,BD=DF,CF=BE,证明:(1)∠C=90°;
(2)AB=AF+2EB.
分析 (1)根据SSS推出△FCD≌△BED,根据全等三角形的性质得出∠C=∠DEB即可;
(2)求出∠C=∠AED=90°,根据HL推出Rt△ACD≌Rt△AED,根据全等三角形的性质得出AC=AE即可.
解答 证明:(1)在△FCD和△BED中,
$\left\{\begin{array}{l}{DF=BD}\\{CF=EB}\\{CD=DE}\end{array}\right.$,
∴△FCD≌△BED(SSS),
∴∠C=∠DEB,
∵DE⊥AB,
∴∠DEB=90°,
∴∠C=90°;
(2)∵DE⊥AB,∠C=90°,
∴∠C=∠AED=90°,
在Rt△ACD和Rt△AED中,
$\left\{\begin{array}{l}{AD=AD}\\{CD=DE}\end{array}\right.$,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
∴AE=AC=AF+CF=AF+BE,
∴AB=AE+BE=AF+BE+BE=AF+2BE.
点评 本题考查了全等三角形的性质和判定,角平分线性质的应用,能根据全等三角形的性质和判定进行推理是解此题的关键.

练习册系列答案
相关题目
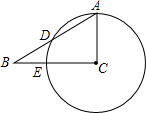 如图,在△ABC中,∠ACB=90°,∠B=36°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E.求弧AD所对的圆心角的度数72°.
如图,在△ABC中,∠ACB=90°,∠B=36°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E.求弧AD所对的圆心角的度数72°. 如图,BD是△ABC的角平分线,∠A=40°,∠ABC=70°,DF⊥BC于F,E为BC延长线上一点,CE=CD,求证:BF=EF.
如图,BD是△ABC的角平分线,∠A=40°,∠ABC=70°,DF⊥BC于F,E为BC延长线上一点,CE=CD,求证:BF=EF.