题目内容
15.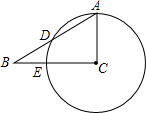 如图,在△ABC中,∠ACB=90°,∠B=36°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E.求弧AD所对的圆心角的度数72°.
如图,在△ABC中,∠ACB=90°,∠B=36°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E.求弧AD所对的圆心角的度数72°.
分析 连接OD,由直角三角形的性质得出∠A=54°,由等腰三角形的性质得出∠ODA=∠A=54°,由三角形内角和定理求出∠ACD即可.
解答 解:连接CD,如图所示:
∵∠ACB=90°,∠B=36°,
∴∠A=90°-∠A=54°,
∵CA=CD,
∴∠CDA=∠A=54°,
∴∠ACD=180°-54°-54°=72°;
故答案为:72°.
点评 本题考查了圆心角、弧、弦的关系、直角三角形的性质、等腰三角形的性质;熟练掌握直角三角形的性质,由等腰三角形的性质求出∠1ACD是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列各数中,最小的是( )
| A. | -1.5 | B. | 0 | C. | 2 | D. | -|-2.5| |
5.若M-1的相反数是3,那么-M的值是( )
| A. | +2 | B. | -2 | C. | +3 | D. | -3 |
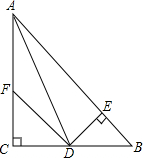 如图所示,在△ABC中,DE⊥AB交AB于E,DE=CD,F在AC上,BD=DF,CF=BE,证明:
如图所示,在△ABC中,DE⊥AB交AB于E,DE=CD,F在AC上,BD=DF,CF=BE,证明: