题目内容

16．计算：（a3+b3+2a2b-1+ab+2ab2）整除（a+b-1）的商式．

分析 首先将原式变形为a3+3a2b+3ab2+b3-a2b-ab2+ab-1，然后利用立方差与立方和公式进行分解，从而可求得商式．

解答 解：原式=a3+3a2b+3ab2+b3-a2b-ab2+ab-1
=（a+b）3-13-ab（a+b-1）
=（a+b-1）[（a+b）2+a+b+1]-ab（a+b-1）
=（a+b-1）（a2+2ab+b2+a+b+1-ab）
=（a+b-1）（a2+ab+b2+a+b+1）．
故商式为：a2+ab+b2+a+b+1．

点评 本题主要考查的是整式的除法，利用立方和与立方差公式分解因式是解题的关键．

练习册系列答案
相关题目
6．写出一个比-5小的有理数-6（答案不唯一）．
7．计算
（1）$（-3\frac{4}{7}）÷（-1\frac{2}{3}）×（-15）÷（-\frac{1}{2}）$
（2）-（-2）4×5-|-32-（-2）4×（-1）9|
（3）20+（-6）+14+（-18）
（4）$0.5+（-\frac{1}{4}）-（-2.75）+\frac{1}{2}$．
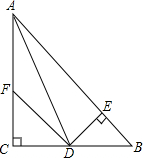4．如图所示，在△ABC中，DE⊥AB交AB于E，DE=CD，F在AC上，BD=DF，CF=BE，证明：
（1）∠C=90°；
（2）AB=AF+2EB．
11．把一张边长为40cm的正方形硬纸板，进行适当的裁剪，折成一个长方体盒子（纸板的厚度忽略不计）．
（1）如图，若在正方形硬纸板的四角各剪掉一个同样大小的正方形，将剩余部分折成一个无盖的长方体盒子．
①要使折成的长方体盒子的底面积为484cm2，那么剪掉的正方形的边长为多少？
②折成的长方体盒子的侧面积是否有最大值？如果有，求出这个最大值和此时剪掉的正方形的边长；如果没有，说明理由．
（2）若在正方形硬纸板的四周剪掉一些矩形（即剪掉的矩形至少有一条边在正方形硬纸板的边上），将剩余部分折成一个有盖的长方体盒子．若折成的一个长方体盒子的表面积为550cm2，求此时长方体盒子的长、宽、高（只需求出符合要求的一种情况）．
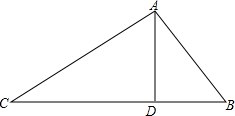1．如图，△ABC中，AD是边CB上的高，且$\frac{CD}{AD}$=$\frac{AD}{BD}$，求∠BAC的大小．
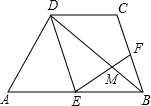8．如图，梯形ABCD中，AB∥CD，且AB=2CD，E、F分别是AB、BC的中点，EF与BD相交于点M．
（1）求证：△EDM∽△FBM；
（2）若△FBM的面积是3，求△BDE的面积．
5．若M-1的相反数是3，那么-M的值是（　　）
A．+2B．-2C．+3D．-3
6．若抛物线y=-x2经过适当的平移后经过点（-1，0）和（2，3），求平移后抛物线的解析式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网