题目内容
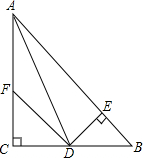
14．
如图，BD是△ABC的角平分线，∠A=40°，∠ABC=70°，DF⊥BC于F，E为BC延长线上一点，CE=CD，求证：BF=EF．
分析 由三角形的内角和定理得到∠ACB=70°，根据角平分线的定义得到∠DBC=$\frac{1}{2}∠$ABC=35°，根据等腰三角形的性质得到∠CDE=∠E=$\frac{1}{2}∠$ACB=35°，证得BD=DE，由等腰三角形三线合一的性质即可得到结论．
解答 证明：∵∠A=40°，∠ABC=70°，
∴∠ACB=70°，
∵BD是△ABC的角平分线，
∴∠DBC=$\frac{1}{2}∠$ABC=35°，
∵CE=CD，
∴∠CDE=∠E=$\frac{1}{2}∠$ACB=35°，
∴∠DBF=∠E，
∴BD=DE，
∵DF⊥BC于F，
∴BF=EF．
点评 本题考查了等腰三角形判定和性质，三角形的内角和，角平分线的性质，熟练掌握等腰三角形判定和性质是解题的关键．
练习册系列答案
金博士一点全通系列答案
相关题目
如图所示，在△ABC中，DE⊥AB交AB于E，DE=CD，F在AC上，BD=DF，CF=BE，证明：
5．若M-1的相反数是3，那么-M的值是（ ）
| A． | +2 | B． | -2 | C． | +3 | D． | -3 |
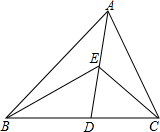如图所示，在△ABC中，AB＞AC，AD为∠BAC的平分线，E为AD上一点，求证：
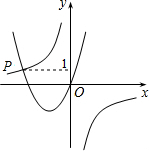如图，已知函数y=-$\frac{3}{x}$与y=ax2+bx（a＞0，b＞0）的图象交于点P（-3，1），则关于x的不等式ax2+bx＞-$\frac{3}{x}$的解为x＜-3或x＞0．
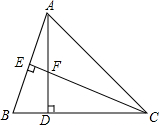已知△ABC中，AD=CD，AD⊥BC，CE⊥AB，垂足分别为D，E，AD与CE相交于F点，且AE=$\frac{1}{2}$CF．求证：CE平分∠ACB．