题目内容
18.如图,已知等边△ABC和点P,设点P到△ABC三边AB、AC、BC(或其延长线)的距离分别为h1、h2、h3,△ABC的高为h.在图(1)中,点P是边BC的中点,此时h3=0,可得结论:h1+h2+h3=h.根据点P所在的不同位置,试探究下列问题:在图(2),(3),(4),(5)中,点P分别在线段MC上、MC延长线上、△ABC内、△ABC外.
(1)如图②,点P在线段MC上,直接写出h1、h2、h3、h之间的关系;
(2)如图③,点P在△ABC内,写出h1、h2、h3、h之间的关系,并说明理由;
(3)如图④,点P在线段MC的延长线上,试猜想h1、h2、h3、h之间存在什么关系?(直接写结论)
(4)如图⑤,点P在△ABC外,写出h1、h2、h3、h之间的关系,并说明理由.

分析 (1)连接AP,根据S△ABC=S△ABP+S△APC可知$\frac{1}{2}$BC•AM=$\frac{1}{2}$AB•PD+$\frac{1}{2}$AC•PF,再把AB=BC=AC及AM=h,PD=h1,PF=h2,代入即可得出结论;
(2)连接AP、BP、CP,根据S△ABC=S△ABP+S△BPC+S△ACP即可得出结论;
(3)连接AP,根据S△ABC=S△ABP-S△APC可知$\frac{1}{2}$BC•AM=$\frac{1}{2}$AB•PD-$\frac{1}{2}$AC•PF,再把AB=BC=AC及AM=h,PD=h1,PF=h2,代入即可得出结论;
(4)连接PB,PC,PA,由三角形的面积公式得:S△ABC=S△PAB+S△PAC-S△PBC,即$\frac{1}{2}$BC•AM=$\frac{1}{2}$AB•PD+$\frac{1}{2}$AC•PE-$\frac{1}{2}$BC•PF,再由AB=BC=AC即可得出结论.
解答 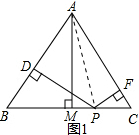 解:(1)h=h1+h2,理由如下:如图1,
解:(1)h=h1+h2,理由如下:如图1,
连接AP,则 S△ABC=S△ABP+S△APC
∴$\frac{1}{2}$BC•AM=$\frac{1}{2}$AB•PD+$\frac{1}{2}$AC•PF
即 $\frac{1}{2}$BC•h=$\frac{1}{2}$AB•h1+$\frac{1}{2}$AC•h2
又∵△ABC是等边三角形
∴BC=AB=AC,
∴h=h1+h2.
故答案为:h=h1+h2.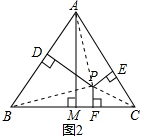
(2)h=h1+h2+h3 ,如图2,理由如下:
连接AP、BP、CP,则 S△ABC=S△ABP+S△BPC+S△ACP
∴$\frac{1}{2}$BC•AM=$\frac{1}{2}$AB•PD+$\frac{1}{2}$AC•PF+$\frac{1}{2}$BC•PE
即 $\frac{1}{2}$BC•h=$\frac{1}{2}$AB•h1+$\frac{1}{2}$AC•h2+$\frac{1}{2}$BC•h3
又∵△ABC是等边三角形,
∴BC=AB=AC.
∴h=h1+h2+h3;
(3)h1-h2=h;如图3,连接AP,
∵S△ABC=S△PAB-S△PAC,
即$\frac{1}{2}$BC•AM=$\frac{1}{2}$AB•PD-$\frac{1}{2}$AC•PE,
∵AB=BC=AC,
∴h1-h2=h,
即h1-h2=h;
(4)h=h1+h2-h3.
当点P在△ABC外时,结论h1+h2+h3=h不成立.此时,它们的关系是h1+h2-h3=h.
理由如下:如图4,连接PB,PC,PA
由三角形的面积公式得:S△ABC=S△PAB+S△PAC-S△PBC,
即$\frac{1}{2}$BC•AM=$\frac{1}{2}$AB•PD+$\frac{1}{2}$AC•PE-$\frac{1}{2}$BC•PF,
∵AB=BC=AC,
∴h1+h2-h3=h,
即h1+h2-h3=h.
点评 本题考查的是等边三角形的性质,根据题意作出辅助线,构造出三角形,根据三角形的面积公式求解是解答此题的关键.

| $\frac{3}{2}$x-y | ||
| x | ||
| 2y |
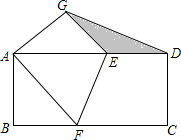 如图,把一张长方形纸片ABCD折叠起来,使其对角顶点A与C重合,D与G重合.若长方形的长BC为8,宽AB为4,求:
如图,把一张长方形纸片ABCD折叠起来,使其对角顶点A与C重合,D与G重合.若长方形的长BC为8,宽AB为4,求: 求出图中的△OPQ中的sinP,cosP,sinQ,cosQ的值.
求出图中的△OPQ中的sinP,cosP,sinQ,cosQ的值.