题目内容
3．平面内有n个点（n＞2且任意3点都不在同一直线上），若从中任意取3个点，以其中一点为端点．且经过另外两点画射线都能构成一个角．（1）若n=3，则能构成角的个数S3=3；
（2）名n=4，则能构成角的个数s4=12；
（3）若n=5，则能构成角的个数S5=30；
（4）试写出n个点能构成角的个数Sn=$\frac{1}{2}$n（n-1）（n-2）．
分析 过不在同一直线上的三点可以确定1个三角形，也就是则能构成角的个数为3；过不在同一直线上的4点可以确定4个三角形，也就是则能构成角的个数为12；过不在同一直线上的5点可以确定10个三角形，也就是则能构成角的个数为30；…由此得出平面内有n个点，取第一个点A有n种取法，取第二个点B有（n-1）种取法．取第三个点C有（n-2）种取法，顺次连接不在同一直线上的三个点可作1个三角形；但△ABC、△ACB、△BAC、△BCA、△CAB、△CBA是同一个三角形，故应除以6，所以得出三角形的个数为$\frac{1}{6}$n（n-1）（n-2），角的个数为$\frac{1}{2}$n（n-1）（n-2），由此得出答案即可．
解答 解：（1）若n=3，则能构成角的个数S3=3；
（2）若n=4，则能构成角的个数s4=12；
（3）若n=5，则能构成角的个数S5=30；
（4）n个点能构成角的个数Sn=$\frac{1}{2}$n（n-1）（n-2）．
故答案为：3，12，30，$\frac{1}{2}$n（n-1）（n-2）．
点评 此题考查图形的变化规律，从简单情形入手，把问题转化为求三角形的个数找出运算规律，进一步利用规律解决问题．
练习册系列答案
阅读快车系列答案
相关题目
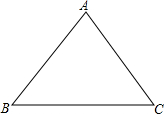请思考如何利用位似变换的思想，在如图的三角形中作一个等边三角形，使它的三个顶点分别在已知三角形的边上，并且等边三角形的一边与BC平行，即：已知△ABC，求作等边△DEF，使它的三个顶点分别在△ABC的边上，且EF∥BC．
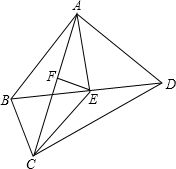如图，在四边形ABCD中，∠BAD=90°，AB=AD=8，BC=4，E是BD的中点，AE=CE．
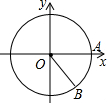如图，以原点为圆心，2为半径的⊙O与正半轴交于点A，在⊙O上且在x轴的下方有一点B，∠AOB=45°，则点B的坐标为（$\sqrt{2}$，$-\sqrt{2}$）．
如图，正方形纸片的边长为20cm，若将其相邻的两边长分别截去xcm和2xcm，求截取后所得的矩形面积y与x之间的函数关系式．