题目内容
9.在如下表所示的空白处填上适当的整式,使每行的3个整式、每列的3个整式、对角的3个整式相加都等于3x.| $\frac{3}{2}$x-y | ||
| x | ||
| 2y |
分析 利用整式的加减首先确定第一行第二列的整式为3x-2y-x=2x-2y,再确定第一行第三列的整式为3x-($\frac{3}{2}$x-y)-(2x-2y)=-$\frac{1}{2}$x+3y,第三确定第三行第一列的整式为3x-(-$\frac{1}{2}$x+3y)-x=$\frac{5}{2}$x-3y,第四确定第二行第一列的为3x-($\frac{5}{2}$x-3y)-($\frac{3}{2}$x-y)=-x+4y,第五确定第二行第三列的整式为3x-x-(-x+4y)=3x-4y,最后得出第三行第三列的整式为3x-x-($\frac{3}{2}$x-y)=$\frac{1}{2}$x+y,由此填表得出答案即可.
解答 解:如表:
| $\frac{3}{2}$x-y | 2x-2y | -$\frac{1}{2}$x+3y |
| -x+4y | x | 3x-4y |
| $\frac{5}{2}$x-3y | 2y | $\frac{1}{2}$x+y |
点评 此题考查整式的加减,理解题意,利用使每行的3个整式、每列的3个整式、对角的3个整式相加都等于3x逐一推算是解决问题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
19.下列选项中,与-$\frac{2}{5}$互为相反数的是( )
| A. | -$\frac{2}{5}$ | B. | $\frac{2}{5}$ | C. | -$\frac{5}{2}$ | D. | $\frac{5}{2}$ |
 如图所示,已知∠B=∠BGD,∠DGF=∠F,求证:AB∥EF.
如图所示,已知∠B=∠BGD,∠DGF=∠F,求证:AB∥EF.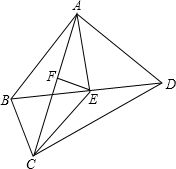 如图,在四边形ABCD中,∠BAD=90°,AB=AD=8,BC=4,E是BD的中点,AE=CE.
如图,在四边形ABCD中,∠BAD=90°,AB=AD=8,BC=4,E是BD的中点,AE=CE. 如图,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,判断⊙D与OA的位置关系,并证明你的结论.
如图,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,判断⊙D与OA的位置关系,并证明你的结论.