题目内容
17.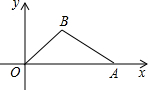 如图,在平面直角坐标系内,O为原点,点A在x轴正半轴上,点B(4,3),
如图,在平面直角坐标系内,O为原点,点A在x轴正半轴上,点B(4,3),(1)求sin∠BOA;
(2)若tan∠BAO=sin∠BOA,求点A的坐标.
分析 (1)作BC⊥OA于C,如图,由B点坐标得到OC=4,BC=3,则根据勾股定理可计算出BC=5,然后根据正弦的定义求解;
(2)利用tan∠BAO=sin∠BOA可得tan∠BAC=$\frac{BC}{AC}$=$\frac{3}{5}$,则可计算出AC=5,所以OA=9,于是可确定点A的坐标.
解答  解:(1)作BC⊥OA于C,如图,
解:(1)作BC⊥OA于C,如图,
∵B(4,3),
∴OC=4,BC=3,
∴BC=$\sqrt{O{C}^{2}+B{C}^{2}}$=5,
∴sin∠BOC=$\frac{BC}{OB}$=$\frac{3}{5}$,
即sin∠BOA=$\frac{3}{5}$;
(2)∵tan∠BAO=sin∠BOA=$\frac{3}{5}$,
∴在Rt△ABC中,tan∠BAC=$\frac{BC}{AC}$=$\frac{3}{5}$,
∴AC=$\frac{5}{3}$×3=5,
∴OA=OC+AC=9,
∴点A的坐标为(9,0).
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了坐标与图形性质.

练习册系列答案
相关题目
12.计算:a-2(1-3a)的结果为( )
| A. | 7a-2 | B. | -2-5a | C. | 4a-2 | D. | 2a-2 |
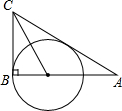 如图,在Rt△ABC中,∠ABC=90°,∠ACB的平分线CO交AB边于点O,以点O为圆心,OB为半径作⊙O.
如图,在Rt△ABC中,∠ABC=90°,∠ACB的平分线CO交AB边于点O,以点O为圆心,OB为半径作⊙O.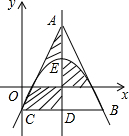 如图,点E是抛物线y=a(x-2)2+k的顶点,抛物线与y轴交于点C,过点C作CD∥x轴,与抛物线交于点B,与对称轴交于点D.点A是对称轴上一点,连结AC、AB.若△ABC是等边三角形,则图中阴影部分图形的面积之和是2$\sqrt{3}$.
如图,点E是抛物线y=a(x-2)2+k的顶点,抛物线与y轴交于点C,过点C作CD∥x轴,与抛物线交于点B,与对称轴交于点D.点A是对称轴上一点,连结AC、AB.若△ABC是等边三角形,则图中阴影部分图形的面积之和是2$\sqrt{3}$. 把一个含有45°角的三角板放在如图所示的两平行线上,测得∠α=120°,则∠β的度数为75°.
把一个含有45°角的三角板放在如图所示的两平行线上,测得∠α=120°,则∠β的度数为75°.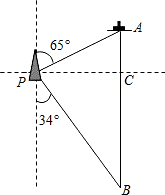 如图,一艘海伦位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海伦所在的B处距离灯塔P有多远?(sin65°≈0.91,cos65°≈0.42,sin34°≈0.56,cos34°≈0.83)
如图,一艘海伦位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海伦所在的B处距离灯塔P有多远?(sin65°≈0.91,cos65°≈0.42,sin34°≈0.56,cos34°≈0.83) 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=8,将△ABC沿CB向右平移得到△DEF.若四边形ABED的面积等于8,则平移距离等于( )
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=8,将△ABC沿CB向右平移得到△DEF.若四边形ABED的面积等于8,则平移距离等于( )