题目内容
7. 如图,在四边形ABCD中,M、N分别是对角线AC、BD的中点,又AD、BC的延长线交于P,求证:S△PMN=$\frac{1}{4}$S四边形ABCD.
如图,在四边形ABCD中,M、N分别是对角线AC、BD的中点,又AD、BC的延长线交于P,求证:S△PMN=$\frac{1}{4}$S四边形ABCD.
分析 先连接DM,BM,根据三角形的中线将三角形分成面积相等的两部分,得到△ADM的面积+△ABM的面积=$\frac{1}{2}$×四边形ABCD的面积,根据三角形的中线将三角形分成面积相等的两部分,得到△BPM的面积=$\frac{1}{2}$×△ABP的面积,最后根据三角形的中线将三角形分成面积相等的两部分,得到△PMN的面积=△BPM的面积-△BPN的面积-△BMN的面积=$\frac{1}{4}$S四边形ABCD.
解答 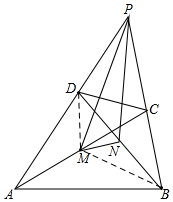 解:如图所示,连接DM,BM,
解:如图所示,连接DM,BM,
∵M是AC的中点,
∴△ADM的面积=$\frac{1}{2}$×△ACD的面积,△ABM的面积=$\frac{1}{2}$×△ACB的面积,
∴△ADM的面积+△ABM的面积=$\frac{1}{2}$(△ACD的面积+△ACB的面积)=$\frac{1}{2}$×四边形ABCD的面积,
∵M是AC的中点,
∴△BPM的面积=△MPC的面积+△MBC的面积
=$\frac{1}{2}$×△ACP的面积+$\frac{1}{2}$×△ABC的面积
=$\frac{1}{2}$×△ABP的面积,
∵N是BD的中点,
∴△BPN的面积=$\frac{1}{2}$×△BDP的面积,△BMN的面积=$\frac{1}{2}$×△BDM的面积,
∴S△PMN=△BPM的面积-△BPN的面积-△BMN的面积
=$\frac{1}{2}$×△ABP的面积-$\frac{1}{2}$×△BDP的面积-$\frac{1}{2}$×△BDM的面积
=$\frac{1}{2}$(△ABP的面积-△BDP的面积-△BDM的面积)
=$\frac{1}{2}$(△ADM的面积+△ABM的面积)
=$\frac{1}{2}$×$\frac{1}{2}$×S四边形ABCD
=$\frac{1}{4}$S四边形ABCD
点评 本题考查的是三角形中线性质的应用,掌握三角形的中线将三角形分成面积相等的两部分是解题的关键.


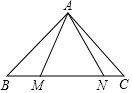 如图,在等腰直角三角形ABC中,∠BAC=90°,AB=AC=15$\sqrt{2}$,点M、N在边BC上,且∠MAN=45°,CN=5,MN=13.
如图,在等腰直角三角形ABC中,∠BAC=90°,AB=AC=15$\sqrt{2}$,点M、N在边BC上,且∠MAN=45°,CN=5,MN=13. 如图,△ABC中,AB=AC,∠BAC=90°,在CB的延长线上取一点D,连接AD,过点A作AE⊥AD,过点C作CE⊥CB,AE与CE交于点E,连接BE,延长△ADC的中线AF交BE于点G.
如图,△ABC中,AB=AC,∠BAC=90°,在CB的延长线上取一点D,连接AD,过点A作AE⊥AD,过点C作CE⊥CB,AE与CE交于点E,连接BE,延长△ADC的中线AF交BE于点G. 如图,在直角坐标系xOy中,点A,B分别在x轴和y轴上,$\frac{OA}{OB}=\frac{3}{4}$,∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=$\frac{k}{x}$的图象过点C,若以CD为边的正方形的面积等于 $\frac{2}{7}$,则k的值是7.
如图,在直角坐标系xOy中,点A,B分别在x轴和y轴上,$\frac{OA}{OB}=\frac{3}{4}$,∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=$\frac{k}{x}$的图象过点C,若以CD为边的正方形的面积等于 $\frac{2}{7}$,则k的值是7.