题目内容
12.任取不等式组$\left\{\begin{array}{l}{k-3≤0}\\{2k+5≥0}\end{array}\right.$的一个整数解,则能使关于x的方程$\frac{k}{x+1}$=$\frac{1}{2}$的解为非正数的概率为$\frac{1}{3}$.分析 先求出不等式组的整数解,再求出x=2k-1,然后把整数解代入,求出x的值,最后根据概率公式即可得出答案.
解答 解:解不等式组$\left\{\begin{array}{l}{k-3≤0}\\{2k+5≥0}\end{array}\right.$得:-$\frac{5}{2}$≤k≤3,则不等式组的整数解是:-2,-1,0,1,2,3,
解$\frac{k}{x+1}$=$\frac{1}{2}$得:x=2k-1,
∵当k=-2时,x=-5,
当k=-1时,x=-3,
当k=0时,x=-1,原方程无解,舍去,
当k=1时,x=1,
当k=2时,x=3,
当k=3时,x=5,
∴能使关于x的方程$\frac{k}{x+1}$=$\frac{1}{2}$的解为非正数的概率为$\frac{2}{6}$=$\frac{1}{3}$;
故答案为:$\frac{1}{3}$.
点评 本题考查了概率公式:随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.也考查了解分式方程和不等式组.

练习册系列答案
相关题目
20.将直线y=2x+1变成y=2x-1经过的变化是( )
| A. | 向上平移2个单位 | B. | 向下平移2个单位 | C. | 向右平移2个单位 | D. | 向左平移2个单位 |
3.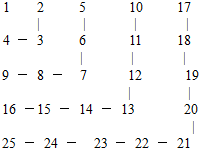 自然数按下表的规律排列,求上起第10行,左起第11列的数是( )
自然数按下表的规律排列,求上起第10行,左起第11列的数是( )
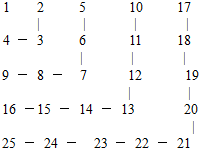 自然数按下表的规律排列,求上起第10行,左起第11列的数是( )
自然数按下表的规律排列,求上起第10行,左起第11列的数是( )| A. | 89 | B. | 90 | C. | 110 | D. | 111 |
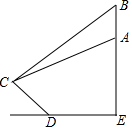 最近央视纪录片《航拍中国》中各地的美景震撼了全国观众,如图是航拍无人机从A点俯拍在坡比为3:4的斜坡CD上的景点C,此时的俯角为30°,为取得更震撼的拍摄效果,无人机升高200米到达B点,此时的俯角变为45°.已知无人机与斜坡CD的坡底D的水平距离DE为400米,则斜坡CD的长度为( )米(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
最近央视纪录片《航拍中国》中各地的美景震撼了全国观众,如图是航拍无人机从A点俯拍在坡比为3:4的斜坡CD上的景点C,此时的俯角为30°,为取得更震撼的拍摄效果,无人机升高200米到达B点,此时的俯角变为45°.已知无人机与斜坡CD的坡底D的水平距离DE为400米,则斜坡CD的长度为( )米(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73) 如图,在四边形ABCD中,M、N分别是对角线AC、BD的中点,又AD、BC的延长线交于P,求证:S△PMN=$\frac{1}{4}$S四边形ABCD.
如图,在四边形ABCD中,M、N分别是对角线AC、BD的中点,又AD、BC的延长线交于P,求证:S△PMN=$\frac{1}{4}$S四边形ABCD.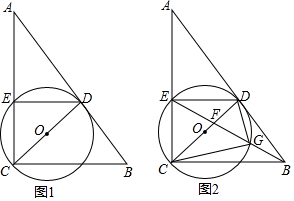
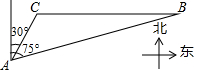 如图,BC是某公园人工湖中的两个人造观光小岛,为了测量两个小岛BC之间的距离,工作人员在距离小岛C 100米的地方选择了一个固定观测点A,并测得小岛C在观侧点A北偏东30°的方向上,与此同时,工作人员还测得小岛B在观测点A北偏东75°的方向上,请你利用工作人员测得的相关数据,计算观光小岛BC之间的距离.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.732,sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.7321)
如图,BC是某公园人工湖中的两个人造观光小岛,为了测量两个小岛BC之间的距离,工作人员在距离小岛C 100米的地方选择了一个固定观测点A,并测得小岛C在观侧点A北偏东30°的方向上,与此同时,工作人员还测得小岛B在观测点A北偏东75°的方向上,请你利用工作人员测得的相关数据,计算观光小岛BC之间的距离.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.732,sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.7321)