题目内容
2. 如图,△ABC中,AB=AC,∠BAC=90°,在CB的延长线上取一点D,连接AD,过点A作AE⊥AD,过点C作CE⊥CB,AE与CE交于点E,连接BE,延长△ADC的中线AF交BE于点G.
如图,△ABC中,AB=AC,∠BAC=90°,在CB的延长线上取一点D,连接AD,过点A作AE⊥AD,过点C作CE⊥CB,AE与CE交于点E,连接BE,延长△ADC的中线AF交BE于点G.求证:AG⊥BE.
分析 如图作AH⊥CD于H.首先证明△DAB≌△EAC,推出BD=EC,由FC=FH+CH=$\frac{BD}{2}$+CH,推出BD=2FH,推出EC=2FH,由$\frac{FG}{EC}$=$\frac{AH}{BC}$=$\frac{1}{2}$,∠AHF=∠BCE,推出△AFH∽△BEC,推出∠FBH=∠FAH,由∠BFG=∠AFH,可得∠BGF=∠AHF=90°.
解答 证明:如图作AH⊥CD于H.
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵CE⊥CD,
∴∠DCE=90°,
∴∠ABD=∠ACE=135°,
∵∠DAE=∠BAC=90°,
∴∠DAB=∠EAC,
∵AB=AC,
∴△DAB≌△EAC,
∴BD=EC,
∵FC=FH+CH=$\frac{BD}{2}$+CH,
∴BD=2FH,
∴EC=2FH,∵BC=2AH,
∴$\frac{FG}{EC}$=$\frac{AH}{BC}$=$\frac{1}{2}$,∵∠AHF=∠BCE,
∴△AFH∽△BEC,
∴∠FBH=∠FAH,
∵∠BFG=∠AFH,
∴∠BGF=∠AHF=90°,
∴AG⊥BE.
点评 本题考查等腰直角三角形的性质、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考压轴题.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
10.下列实数中,无理数是( )
| A. | 2 | B. | -$\frac{1}{2}$ | C. | 3.14 | D. | $\sqrt{3}$ |
13.计算(x4+1)(x2+1)(x+1)(x-1)的结果是( )
| A. | x8+1 | B. | (x+1)8 | C. | x8-1 | D. | (x-1)8 |
14.M(a,b)是一次函数y=x+3图象上一点,则关于x的方程ax2+bx+1=0根的情况是( )
| A. | 没有实数根 | B. | 有实数根 | ||
| C. | 有两个相等的实数根 | D. | 有两个不相等的实数根 |
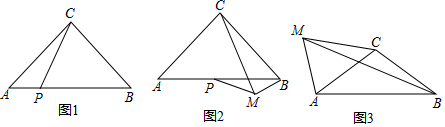
 如图,在四边形ABCD中,M、N分别是对角线AC、BD的中点,又AD、BC的延长线交于P,求证:S△PMN=$\frac{1}{4}$S四边形ABCD.
如图,在四边形ABCD中,M、N分别是对角线AC、BD的中点,又AD、BC的延长线交于P,求证:S△PMN=$\frac{1}{4}$S四边形ABCD. 如图,△ABC中,∠C=90°,AC=8,BC=6,将点C折叠到AB边的点E处,折痕为BD,则CD的长等于3.
如图,△ABC中,∠C=90°,AC=8,BC=6,将点C折叠到AB边的点E处,折痕为BD,则CD的长等于3.