题目内容
18.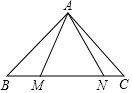 如图,在等腰直角三角形ABC中,∠BAC=90°,AB=AC=15$\sqrt{2}$,点M、N在边BC上,且∠MAN=45°,CN=5,MN=13.
如图,在等腰直角三角形ABC中,∠BAC=90°,AB=AC=15$\sqrt{2}$,点M、N在边BC上,且∠MAN=45°,CN=5,MN=13.
分析 由等腰直角三角形的性质得出∠ABC=∠C=45°,BC=$\sqrt{2}$AB=30,把△ACN绕点A顺时针旋转90°得到△ABD,由旋转的性质得出∠ABD=∠C=45°,BD=CN=5,∠DAN=90°,AD=AN,求出∠DBM=90°,证出∠MAD=∠MAN,由SAS证明△AMD≌△AMN,得出MD=MN,设MD=MN=x,则BM=BC-MN-CN=25-x,在Rt△DBM中,由勾股定理得出方程,解方程即可.
解答 解:∵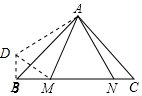 等腰直角三角形ABC中,∠BAC=90°,AB=AC=15$\sqrt{2}$,
等腰直角三角形ABC中,∠BAC=90°,AB=AC=15$\sqrt{2}$,
∴∠ABC=∠C=45°,BC=$\sqrt{2}$AB=30,
把△ACN绕点A顺时针旋转90°得到△ABD,连接MD,如图所示:
则∠ABD=∠C=45°,BD=CN=5,∠DAN=90°,AD=AN,
∴∠DBM=45°+45°=90°,
∵∠MAN=45°,
∴∠MAD=90°-45°=45°,
∴∠MAD=∠MAN,
在△AMD和△AMN中,$\left\{\begin{array}{l}{AD=AN}&{\;}\\{∠MAD=∠MAN}&{\;}\\{AB=AC}&{\;}\end{array}\right.$,
∴△AMD≌△AMN(SAS),
∴MD=MN,
设MD=MN=x,
则BM=BC-MN-CN=25-x,
在Rt△DBM中,由勾股定理得:BD2+BM2=MD2,
即52+(25-x)2=x2,解得:x=13,
∴MN=13;
故答案为:13.
点评 本题考查了全等三角形的判定和性质、勾股定理、等腰直角三角形的性质,题目的综合性较强,难度较大,解题的关键是正确的作出辅助线构造全等三角形.

练习册系列答案
相关题目
6.计算(-4)×(-3)的结果等于( )
| A. | -12 | B. | -7 | C. | 7 | D. | 12 |
7.已知扇形的半径为6cm,圆心角为120°,则这个扇形的面积是( )
| A. | 36πcm2 | B. | 12πcm2 | C. | 9πcm2 | D. | 6πcm2 |
13.计算(x4+1)(x2+1)(x+1)(x-1)的结果是( )
| A. | x8+1 | B. | (x+1)8 | C. | x8-1 | D. | (x-1)8 |
3.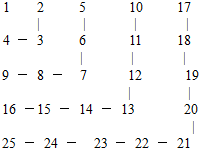 自然数按下表的规律排列,求上起第10行,左起第11列的数是( )
自然数按下表的规律排列,求上起第10行,左起第11列的数是( )
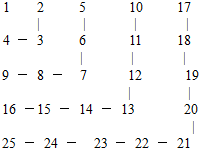 自然数按下表的规律排列,求上起第10行,左起第11列的数是( )
自然数按下表的规律排列,求上起第10行,左起第11列的数是( )| A. | 89 | B. | 90 | C. | 110 | D. | 111 |
8.点A在x轴正半轴上,且距y轴的距离是3,则点A的坐标是( )
| A. | (3,0) | B. | (-3,0) | C. | (0,3) | D. | (0,-3) |
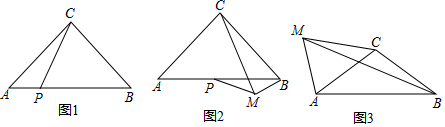
 如图,在四边形ABCD中,M、N分别是对角线AC、BD的中点,又AD、BC的延长线交于P,求证:S△PMN=$\frac{1}{4}$S四边形ABCD.
如图,在四边形ABCD中,M、N分别是对角线AC、BD的中点,又AD、BC的延长线交于P,求证:S△PMN=$\frac{1}{4}$S四边形ABCD.