题目内容
6. 先阅读材料,解答下列问题:
先阅读材料,解答下列问题:我们已经知道,多项式与多项式相乘的法则可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,例如:等式(a+2b)(2a+b)=2a2+5ab+2b2就可以用图形①的面积来表示.
(1)请写出图②所表示的代数恒等式(2a+b)(a+b)=2a2+3ab+b2.
(2)画出一个几何图形,使它的面积能表示(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(3)请仿照上述方法写出另一个含a、b的代数恒等式,并画出与之对应的几何图形.
分析 (1)根据长为2a+b、宽为a+2b的矩形面积等于2个边长为a的正方形、1个边长为b的正方形、3个长为a宽为b的矩形面积和,可得等式;
(2)画一个边长为a+b+c的正方形,即可得;
(3)不唯一,如:(x+p)(x+q)=x2+(p+q) x+pq,画长为x+q、宽为x+p的矩形即可得.
解答 解:(1)(2a+b)(a+b)=2a2+3ab+b2;
(2)如图①,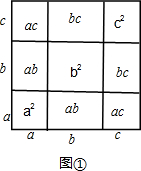
(3)(x+p)(x+q)=x2+(p+q) x+pq,
如图②,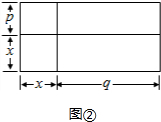
故答案为:(1)(2a+b)(a+b)=2a2+3ab+b2.
点评 本题主要考查了完全平方公式的几何背景,应从整体和部分两方面来理解完全平方公式的几何意义;主要围绕图形面积展开分析.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.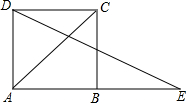 如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E=( )
如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E=( )
 如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E=( )
如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E=( )| A. | 45° | B. | 30° | C. | 22.5° | D. | 15° |
16.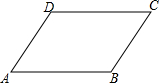 如图,在平行四边形ABCD中,如果∠A=50°,则∠C=( )
如图,在平行四边形ABCD中,如果∠A=50°,则∠C=( )
 如图,在平行四边形ABCD中,如果∠A=50°,则∠C=( )
如图,在平行四边形ABCD中,如果∠A=50°,则∠C=( )| A. | 40° | B. | 50° | C. | 130° | D. | 150° |
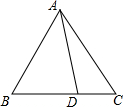 如图,在△ABC中,AB=AC,点D为一边上一点,请你用量角器,在BC边上确定E,使CE=BD,简述你的作法.并说明理由.
如图,在△ABC中,AB=AC,点D为一边上一点,请你用量角器,在BC边上确定E,使CE=BD,简述你的作法.并说明理由.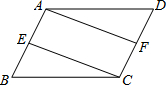 如图,在?ABCD中,E,F分别是AB,CD的中点,连接AF,CE.
如图,在?ABCD中,E,F分别是AB,CD的中点,连接AF,CE. 如图,在Rt△ABC中,∠ACB=90°,AC=$\sqrt{3}$,BC=1,以B为圆心,BC长为半径作弧,交AB于点D,则阴影部分的面积为$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$(结果保留π)
如图,在Rt△ABC中,∠ACB=90°,AC=$\sqrt{3}$,BC=1,以B为圆心,BC长为半径作弧,交AB于点D,则阴影部分的面积为$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$(结果保留π) 如图,在等腰△ABC中,AB=AC=8,BC=6,AB的垂直平分线MN交AC于点D,则△DBC的周长为14.
如图,在等腰△ABC中,AB=AC=8,BC=6,AB的垂直平分线MN交AC于点D,则△DBC的周长为14.