题目内容
19.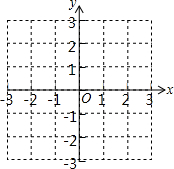 我们知道对于x轴上的任意两点A(x1,0),B(x2,0),有AB=|x1-x2|,而对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1-x2|+|y1-y2|称为Pl,P2两点间的直角距离,记作d(P1,P2),即d(P1,P2)=|x1-x2|+|y1-y2|.
我们知道对于x轴上的任意两点A(x1,0),B(x2,0),有AB=|x1-x2|,而对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1-x2|+|y1-y2|称为Pl,P2两点间的直角距离,记作d(P1,P2),即d(P1,P2)=|x1-x2|+|y1-y2|.(1)已知O为坐标原点,若点P坐标为(1,3),则d(O,P)=4;
(2)已知O为坐标原点,动点P(x,y)满足d(O,P)=2,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形;
(3)试求点M(2,3)到直线y=x+2的最小直角距离.
分析 (1)由P0与原点O的坐标,利用题中的新定义计算即可得到结果;
(2)利用题中的新定义列出x与y的关系式,画出相应的图象即可;
(3)根据新的运算规则知d(M,Q)=|x-2|+|y-3|=|x-2|+|x+2-3|=|x-2|+|x-1|,然后由绝对值与数轴的关系可知,|x-2|+|x-1|表示数轴上实数x所对应的点到数2和1所对应的点的距离之和,其最小值为1.
解答  解:(1)d(O,P)=|0-1|+|0-3|=4;
解:(1)d(O,P)=|0-1|+|0-3|=4;
故答案为:4;
(2)∵O为坐标原点,动点P(x,y)满足d(O,P),
∴|0-x|+|0-y|=|x|+|y|=2,
所有符合条件的点P组成的图形如图所示;
(3)∵d=|x-2|+|y-3|=|x-2|+|x+2-3|
=|x-2|+|x-1|
∴x可取一切实数,|x-2|+|x-1|表示数轴上实数x所对应的点到1和2所对应的点的距离之和,其最小值为1.
∴点M(2,3)到直线y=x+2的直角距离为1.
点评 此题主要考查了一次函数图象,涉及的知识有:绝对值的代数意义,弄清题中的新定义是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.计算(-2x2)2•(-3x)3的结果是( )
| A. | 40x7 | B. | -40x7 | C. | -108x7 | D. | 400x7 |
8.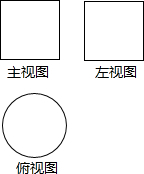 如图所示是一个几何体的三视图,这个几何体的名称是( )
如图所示是一个几何体的三视图,这个几何体的名称是( )
 如图所示是一个几何体的三视图,这个几何体的名称是( )
如图所示是一个几何体的三视图,这个几何体的名称是( )| A. | 圆柱 | B. | 三棱锥 | C. | 球 | D. | 圆锥 |
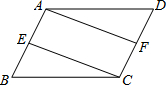 如图,在?ABCD中,E,F分别是AB,CD的中点,连接AF,CE.
如图,在?ABCD中,E,F分别是AB,CD的中点,连接AF,CE.
 如图,在等腰△ABC中,AB=AC=8,BC=6,AB的垂直平分线MN交AC于点D,则△DBC的周长为14.
如图,在等腰△ABC中,AB=AC=8,BC=6,AB的垂直平分线MN交AC于点D,则△DBC的周长为14.