题目内容
5．
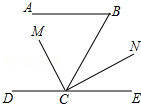已知AB∥DE，∠B=68°，且CM平分∠DCB，CM⊥CN，垂足为C，求∠NCE的度数．
分析 先根据平行线的性质得出∠BCD的度数，再由角平分线的定义求出∠DCM的度数，根据CM⊥CN可知∠MCN=90°，故∠DCM+∠NCE=90°，由此可得出结论．
解答 解：∵AB∥DE，∠B=68°，
∴∠BCD=112°．
∵CM平分∠DCB，
∴∠DCM=$\frac{1}{2}$∠DCB=54°．
∵CM⊥CN，
∴∠MCN=90°，
∴∠DCM+∠NCE=90°，
∴∠NCE=90°-54°=34°．
点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，同旁内角互补．
练习册系列答案
相关题目
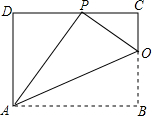如图，将矩形ABCD折叠，使得顶点B落在CD边上的P点处，折痕与边BC交于点O，AD=8，连结AP、OP、OA．
如图，BA⊥AC，点D在AC边上，DE∥BC，若∠1=155°，则∠B的度数为65°．