题目内容
13．在Rt△ABC中，∠ACB=90°，CD⊥AB于D．若BC=3，AC=4，则tan∠BCD的值为$\frac{3}{4}$．分析 根据余角的性质，可得∠BCD=∠A，根据等角的正切相等，可得答案．
解答 解：由∠ACB=90°，CD⊥AB于D，得
∠BCD=∠A
tan∠BCD=tan∠A=$\frac{BC}{AC}$=$\frac{3}{4}$，
故答案为：$\frac{3}{4}$．
点评 本题考查了锐角三角函数的定义，利用余角的性质得出∠BCD=∠A是解题关键．
练习册系列答案
相关题目
3．
根据如图所示的程序计算，若输入x的值为1，则输出y的值为（ ）
根据如图所示的程序计算，若输入x的值为1，则输出y的值为（ ）| A． | 4 | B． | -2 | C． | 8 | D． | 3 |
如图，在△ABC中，AD⊥BC，垂足为D，E为AC上一点，BE交AD于F，且BF=AC，FD=CD，AD=3，求AB的长．
如图，点D、E分别为△ABC的边AB、AC的中点，同时，点F在DE上，且∠AFB=90°，已知AB=5，BC=8，那么EF的长为1.5．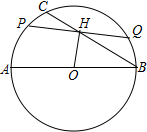
在⊙O中，直径AB=8，∠ABC=30°，点H在弦BC上，弦PQ⊥OH于点H．当点P在$\widehat{AC}$上移动时，PQ长的最大值为4$\sqrt{3}$．