题目内容
14.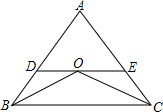 如图,已知OB、OC为△ABC的角平分线,DE∥BC,△ADE的周长为10,BC长为8,求△ABC的周长.
如图,已知OB、OC为△ABC的角平分线,DE∥BC,△ADE的周长为10,BC长为8,求△ABC的周长.
分析 由OB、OC为△ABC的角平分线,DE∥BC交AB、AC于D、E,易得△BOD与△COE是等腰三角形,继而可得DE=BD+EC;易得AD+DE+AE=AD+OD+OE+AE=AD+BD+CE+AE=AB+AC=10,继而求得答案.
解答 解:∵OB、OC为△ABC的角平分线,
∴∠ABO=∠OBC,∠ACO=∠BCO,
∵DE∥BC,
∴∠DOB=∠OBC,∠EOC=∠OCB,
∴∠ABO=∠DOB,∠ACO=∠EOC,
∴BD=OD,EC=OE,
∴DE=OD+OE=BD+EC;
∵△ADE的周长为10,
∴AD+DE+AE=AD+OD+OE+AE=AD+BD+CE+AE=AB+AC=10,
∵BC=8,
∴△ABC的周长为:AB+AC+BC=10+8=18.
点评 本题考查了等腰三角形的判定与性质.此题难度适中,注意掌握转化思想与数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.在启东历史上第一个夺取国际中学生数学奥林匹克竞赛金牌的启东学子是( )
| A. | 陈建鑫 | B. | 毛泽东 | C. | 莫言 | D. | 祖冲之 |
3.若△ABC∽△A′B′C′,∠A=20°,∠C=120°,则∠B′的度数为( )
| A. | 20° | B. | 30° | C. | 40° | D. | 120° |
4.已知二次函数y=3x2+c与正比例函数y=4x的图象只有一个交点,则c的值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | 3 | D. | 4 |
 如图,在△ABC中,AD⊥BC,垂足为D,E为AC上一点,BE交AD于F,且BF=AC,FD=CD,AD=3,求AB的长.
如图,在△ABC中,AD⊥BC,垂足为D,E为AC上一点,BE交AD于F,且BF=AC,FD=CD,AD=3,求AB的长. 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=25°,那么∠2的度数是20°.
如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=25°,那么∠2的度数是20°.
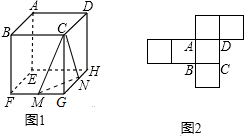 如图,正方体(图1)的展开图如图2所示,在图1中M、N分别是FG、GH的中点,CM、CN、MN是三条线段;请在图2中画出CM、CN、MN这三条线段
如图,正方体(图1)的展开图如图2所示,在图1中M、N分别是FG、GH的中点,CM、CN、MN是三条线段;请在图2中画出CM、CN、MN这三条线段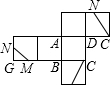 .
.