题目内容
6.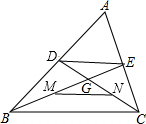 如图,在△ABC中,中线BE与中线CD交于点G,若M为BE的中点,N为CD的中点,则$\frac{MN}{DE}$=$\frac{1}{2}$.
如图,在△ABC中,中线BE与中线CD交于点G,若M为BE的中点,N为CD的中点,则$\frac{MN}{DE}$=$\frac{1}{2}$.
分析 根据题意得到点G是△ABC的重心,根据重心的性质和题意得到$\frac{NG}{GD}$=$\frac{MG}{GE}$=$\frac{1}{2}$,得到答案.
解答 解:∵点G是△ABC的重心,
∴CG=2DG,BG=2GE,
∵M为BE的中点,N为CD的中点,
∴$\frac{NG}{GD}$=$\frac{MG}{GE}$=$\frac{1}{2}$,
∴$\frac{MN}{DE}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查的是三角形的重心的概念和性质,三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
16.下列图形中,不是轴对称图形的有( )
| A. |  | B. |  | C. |  | D. |  |
 如图,⊙O的$\widehat{CB}=2\widehat{AB}$,∠BOC=72°,则∠OAB=72°.
如图,⊙O的$\widehat{CB}=2\widehat{AB}$,∠BOC=72°,则∠OAB=72°. 如图,已知AB是⊙O的直径,AB=10,点C、D在⊙O上,DC平分∠ACB,点E在⊙O外,
如图,已知AB是⊙O的直径,AB=10,点C、D在⊙O上,DC平分∠ACB,点E在⊙O外,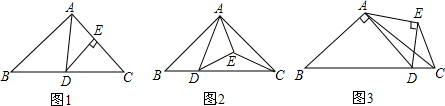
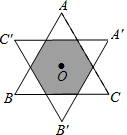 如图,已知等边三角形的面积为1,O为△ABC的中心(O到△ABC的各边距离相等),将△ABC绕中心O旋转60°,得到△A′B′C′,则△ABC与△A′B′C′重叠部分的面积为$\frac{2}{3}$.
如图,已知等边三角形的面积为1,O为△ABC的中心(O到△ABC的各边距离相等),将△ABC绕中心O旋转60°,得到△A′B′C′,则△ABC与△A′B′C′重叠部分的面积为$\frac{2}{3}$.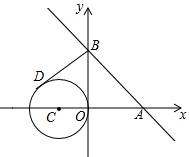 如图,直线y=-x+2与x轴、y轴分别交于点A,B,C(-1,0),且圆C的半径为1.若BD切圆C于点D,点D在第二象限,求点D的坐标.
如图,直线y=-x+2与x轴、y轴分别交于点A,B,C(-1,0),且圆C的半径为1.若BD切圆C于点D,点D在第二象限,求点D的坐标.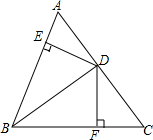 如图,BD平分∠ABC,DE⊥AB于E,DF⊥BC于F,AB=12,BC=18.
如图,BD平分∠ABC,DE⊥AB于E,DF⊥BC于F,AB=12,BC=18.