题目内容
15．
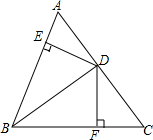如图，BD平分∠ABC，DE⊥AB于E，DF⊥BC于F，AB=12，BC=18．（1）求S△ABD：S△BCD的值；
（2）若S△ABC=36，求DE的长．
分析 （1）根据角平分线的性质得到DE=DF，根据三角形的面积公式计算即可得到答案；
（2）根据三角形的面积公式计算即可求出DE的长．
解答 解：（1）∵BD平分∠ABC，DE⊥AB于E，DF⊥BC于F，
∴DE=DF，
∴S△ABD：S△BCD=$\frac{\frac{1}{2}×AB×DE}{\frac{1}{2}×BC×DF}$=2：3；
（2）S△ABC=S△ABD+S△BCD=$\frac{1}{2}$×AB×DE+$\frac{1}{2}$×BC×DF=36，
解得DE=$\frac{12}{5}$．
点评 本题考查的是角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．
练习册系列答案
相关题目
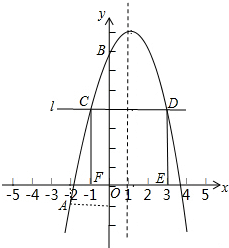如图，已知二次函数y=-x2+bx+c的图象经过A（-2，-1），B（0，7）两点．
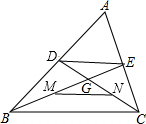如图，在△ABC中，中线BE与中线CD交于点G，若M为BE的中点，N为CD的中点，则$\frac{MN}{DE}$=$\frac{1}{2}$．
如图，BE、CE分别为△ABC的两个外角平分线，EP⊥AM于P，EQ⊥AN于Q