题目内容
1．
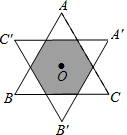如图，已知等边三角形的面积为1，O为△ABC的中心（O到△ABC的各边距离相等），将△ABC绕中心O旋转60°，得到△A′B′C′，则△ABC与△A′B′C′重叠部分的面积为$\frac{2}{3}$．
分析 根据重合部分时正六边形，连接O和正六边形的各个顶点，所得的三角形都是全等的等边三角形，据此即可求解．
解答 
解：重合部分时正六边形，连接O和正六边形的各个顶点，所得的三角形都是全等的等边三角形．
则S阴影=$\frac{6}{9}$S△ABC=$\frac{6}{9}$=$\frac{2}{3}$．
故答案是：$\frac{2}{3}$．
点评 本题考查了等边三角形的性质以及旋转的性质，理解连接O和正六边形的各个顶点，所得的三角形都是全等的等边三角形是关键．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
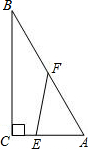如图，在Rt△ABC中，∠C=90°，AC=3，BC=4，点E是直角边AC上动点（点E与A、C两点均不重合），点F是斜边AB上的动点（点F与A、B两点均不重合）．设AE长为x．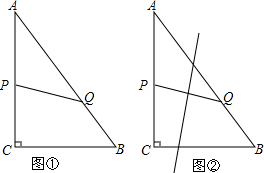
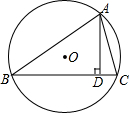如图，O是△ABC的外心，AD是BC边上的高，R是△ABC外接圆的半径．问：
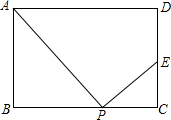在矩形ABCD中，AB=4，AD=7，P是边BC上的任意一点（P与B、C不重合），作PE⊥AP，交CD边所在于点E．
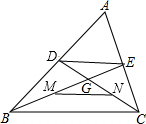如图，在△ABC中，中线BE与中线CD交于点G，若M为BE的中点，N为CD的中点，则$\frac{MN}{DE}$=$\frac{1}{2}$．
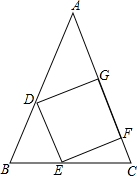已知，如图，正方形DEFG的一边FG在等腰△ABC的腰AC上，AB=AC=5，顶点D、E分别为边AB、BC上，△ABC的面积为10，求正方形DEFG的面积．
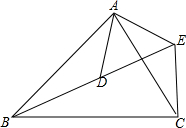如图，AB：AD=BC：DE=AC：AE．