题目内容
4.正△与边长相等的正n边形进行平面镶嵌,则n=6.分析 设正多边形的每个内角为x,根据正三角形的每个内角为60°,求出正多边形的每个内角度数,然后求出正多边形的每个外角的度数,用外角之和除以每个外角的度数即可得出答案.
解答 解:设正多边形的每个内角为x,
∵正三角形的每个内角为60°,
∴60+x=360,
∴x=300,
∴正多边形的每个外角是60°,
∴n=360÷60=6;
故答案为:6
点评 此题考查了平面镶嵌,解答此题的关键是看位于同一顶点处的几个角之和能否为360°.若能,则说明可以进行平面镶嵌;反之,则说明不能进行平面镶嵌.

练习册系列答案
相关题目
12.女生人数占男生人数的$\frac{4}{5}$,男生人数占女生人数的( )
| A. | $\frac{1}{4}$ | B. | $\frac{5}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{4}{5}$ |
13.平行四边形一边长为12cm,那么它的两条对角线的长度可能是( )
| A. | 8cm和14cm | B. | 10cm和14cm | C. | 10cm和34cm | D. | 18cm和20cm |
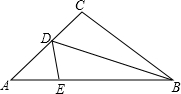 如图所示,三角形纸片ABC,AB=10厘米,BC=7厘米,AC=6厘米.沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为9厘米.
如图所示,三角形纸片ABC,AB=10厘米,BC=7厘米,AC=6厘米.沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为9厘米.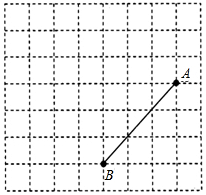 (1)请在网格中建立平面直角坐标系,使得A,B两点的坐标分别为(4,1),(1,-2);
(1)请在网格中建立平面直角坐标系,使得A,B两点的坐标分别为(4,1),(1,-2);