题目内容
9.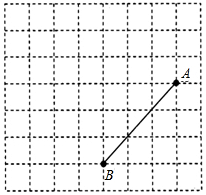 (1)请在网格中建立平面直角坐标系,使得A,B两点的坐标分别为(4,1),(1,-2);
(1)请在网格中建立平面直角坐标系,使得A,B两点的坐标分别为(4,1),(1,-2);(2)在(1)的条件下,过点B作x轴的垂线,垂足为点M,在BM的延长线上截取MC=BM.
①写出点M的坐标;
②平移线段AB使点A移动到点C,画出平移后的线段CD,并写出点D的坐标.
③若P为x轴上一点,且S△PBD=3,求P点坐标.
分析 (1)根据点A、B坐标即可建立坐标系;
(2)①由(1)中所作图形即可得;②根据平移的定义作图可得;设点P坐标为(a,0),根据S△PBO=3利用三角形面积公式建立方程求解可得.
解答 解:(1)建立平面直角坐标系如图所示: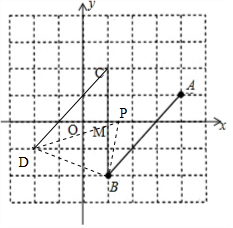
(2)①由图可知点M坐标为(1,0);
②如图所示,线段CD即为所求,点D的坐标为(-2,-1);
③设点P坐标为(a,0),
∵S△PBD=3,
∴$\frac{1}{2}$×(|a+2|+3)×2-$\frac{1}{2}$×1×3+$\frac{1}{2}$×1×|a+2|=3,
解得:a=1或a=-5,
则点P的坐标为(1,0)或(-5,0).
点评 本题主要考查坐标与图形的性质及三角形的面积,熟练掌握平面直角坐标系内点的坐标特点及三角形的面积公式是解题的关键.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
17.一个数的$\frac{3}{11}$是12,这个数的$\frac{3}{4}$是( )
| A. | $\frac{27}{11}$ | B. | $\frac{48}{11}$ | C. | 33 | D. | $\frac{176}{3}$ |
19. 如图,直线AB、CD相交于点O,OA平分∠EOC,∠BOD=28°,则∠EOC的度数等于( )
如图,直线AB、CD相交于点O,OA平分∠EOC,∠BOD=28°,则∠EOC的度数等于( )
 如图,直线AB、CD相交于点O,OA平分∠EOC,∠BOD=28°,则∠EOC的度数等于( )
如图,直线AB、CD相交于点O,OA平分∠EOC,∠BOD=28°,则∠EOC的度数等于( )| A. | 28° | B. | 40° | C. | 50° | D. | 56° |
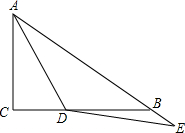 如图:Rt△ACB中,∠ACB=90°,AD平分∠CAB交BC于D,点E在AB的延长线上,满足∠ADE+∠CAB=180°.已知AC=6,BE=2,求线段BD的长为5.
如图:Rt△ACB中,∠ACB=90°,AD平分∠CAB交BC于D,点E在AB的延长线上,满足∠ADE+∠CAB=180°.已知AC=6,BE=2,求线段BD的长为5.