题目内容
已知⊙O1的半径r1=2,⊙O2的半径r2是方程
=
的根,当两圆相内切时,⊙O1与⊙O2的圆心距为( )
| 3 |
| x |
| 2 |
| x-1 |
| A、5 | B、4 | C、1或5 | D、1 |
考点:圆与圆的位置关系,解分式方程
专题:
分析:首先解分式方程,求得⊙O2的半径r2,又由⊙O1的半径r1=2,两圆相内切,根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系即可求得答案.
解答:解:方程两边同乘以x(x-1)得:3(x-1)=2x,
解得:x=3,
经检验,x=3是原分式方程的解;
∴r2=3,
∵⊙O1的半径r1=2,且两圆相内切,
∴⊙O1与⊙O2的圆心距为:3-2=1.
故选D.
解得:x=3,
经检验,x=3是原分式方程的解;
∴r2=3,
∵⊙O1的半径r1=2,且两圆相内切,
∴⊙O1与⊙O2的圆心距为:3-2=1.
故选D.
点评:此题考查了圆与圆的位置关系以及分式方程的解法.此题难度不大,注意掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系是解此题的关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
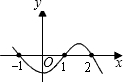 已知y是关于x的函数,函数图象如图,则当y>0时,自变量x的取值范围是( )
已知y是关于x的函数,函数图象如图,则当y>0时,自变量x的取值范围是( )| A、x<0 |
| B、-1<x<1或x>2 |
| C、x>-1 |
| D、x<-1或1<x<2 |
已知|x+y|+(x-y+5)2=0,那么x和y的值分别是( )
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
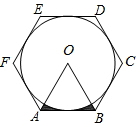 如图,⊙O的外切正六边形ABCDEF的边长为1,则图中阴影部分的面积为( )
如图,⊙O的外切正六边形ABCDEF的边长为1,则图中阴影部分的面积为( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
安徽省有682000名初中毕业生参加中考,按四舍五入保留两位有效数字,682000用科学记数法表示为( )
| A、0.69×106 |
| B、6.82×1 05 |
| C、0.68×106 |
| D、6.8×105 |
 已知反比例函数y=
已知反比例函数y=