题目内容
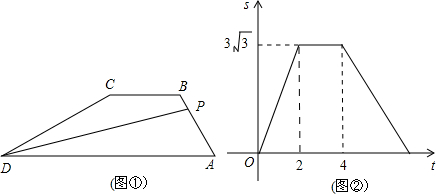
如图①,在梯形ABCD中,AD∥BC,∠A=60°,动点P从A点出发,以1cm/s的速度沿着A→B→C→D的方向不停移动,直到点P到达点D后才停止.已知△PAD的面积S (单位:cm2)与点P移动的时间t(单位:s)的函数关系如图②,则:
(1)BC=2cm;(2)梯形的面积是3
cm2;(3)∠ADC=30°;(4)点P从开始移动到停止移动一共用了7秒.
说法中正确的个数是( )
(1)BC=2cm;(2)梯形的面积是3
| 3 |
说法中正确的个数是( )

| A、1个 | B、2个 | C、3个 | D、4个 |
考点:动点问题的函数图象
专题:
分析:根据图②判断出AB、BC的长度,过点B作BE⊥AD于点E,然后求出梯形ABCD的高BE,再根据t=2时△PAD的面积求出AD的长度,过点C作CF⊥AD于点F,然后求出DF的长度,利用勾股定理列式求出CD的长度,然后求出AB、BC、CD的和,再根据时间=路程÷速度计算即可得解.
解答: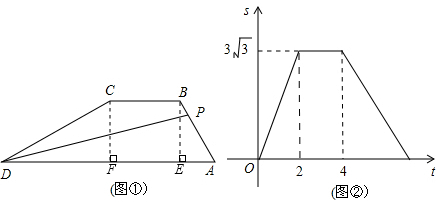 解:由图②可知,t在2到4秒时,△PAD的面积不发生变化,
解:由图②可知,t在2到4秒时,△PAD的面积不发生变化,
∴在AB上运动的时间是2秒,在BC上运动的时间是4-2=2秒,
∵动点P的运动速度是1cm/s,
∴AB=2cm,BC=2cm.
故(1)正确.
从图②知,3
cm2是△PAD的面积,不是梯形ABCD的面积.
故(2)错误;
如图,过点B作BE⊥AD于点E,过点C作CF⊥AD于点F,
则四边形BCFE是矩形,
∴BE=CF,BC=EF=2cm,
∵∠A=60°,
∴BE=ABsin60°=2×
=
,
AE=ABcos60°=2×
=1,
∴
×AD×BE=3
,
即
×AD×
=3
,
解得AD=6cm,
∴DF=AD-AE-EF=6-1-2=3,
在Rt△CDF中,CD=
=
=2
,
所以,动点P运动的总路程为AB+BC+CD=2+2+2
=4+2
,
∵动点P的运动速度是1cm/s,
∴点P从开始移动到停止移动一共用了(4+2
)÷1=4+2
(秒).
故(4)错误;
∵tan∠CDF=
=
=
,
∴∠CDF=30°.
故(3)正确.
综上所述,正确的结论有2个.
故选:B.
 解:由图②可知,t在2到4秒时,△PAD的面积不发生变化,
解:由图②可知,t在2到4秒时,△PAD的面积不发生变化,∴在AB上运动的时间是2秒,在BC上运动的时间是4-2=2秒,
∵动点P的运动速度是1cm/s,
∴AB=2cm,BC=2cm.
故(1)正确.
从图②知,3
| 3 |
故(2)错误;
如图,过点B作BE⊥AD于点E,过点C作CF⊥AD于点F,
则四边形BCFE是矩形,
∴BE=CF,BC=EF=2cm,
∵∠A=60°,
∴BE=ABsin60°=2×
| ||
| 2 |
| 3 |
AE=ABcos60°=2×
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 3 |
即
| 1 |
| 2 |
| 3 |
| 3 |
解得AD=6cm,
∴DF=AD-AE-EF=6-1-2=3,
在Rt△CDF中,CD=
| CF2+DF2 |
| 3+9 |
| 3 |
所以,动点P运动的总路程为AB+BC+CD=2+2+2
| 3 |
| 3 |
∵动点P的运动速度是1cm/s,
∴点P从开始移动到停止移动一共用了(4+2
| 3 |
| 3 |
故(4)错误;
∵tan∠CDF=
| CF |
| DF |
| ||
| 6-1-2 |
| ||
| 3 |
∴∠CDF=30°.
故(3)正确.
综上所述,正确的结论有2个.
故选:B.
点评:本题考查了动点问题的函数图象,根据图②的三角形的面积的变化情况判断出AB、BC的长度是解题的关键,根据梯形的问题中,经常作过梯形的上底边的两个顶点的高线作出辅助线也很关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
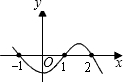 已知y是关于x的函数,函数图象如图,则当y>0时,自变量x的取值范围是( )
已知y是关于x的函数,函数图象如图,则当y>0时,自变量x的取值范围是( )| A、x<0 |
| B、-1<x<1或x>2 |
| C、x>-1 |
| D、x<-1或1<x<2 |
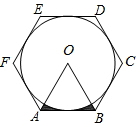 如图,⊙O的外切正六边形ABCDEF的边长为1,则图中阴影部分的面积为( )
如图,⊙O的外切正六边形ABCDEF的边长为1,则图中阴影部分的面积为( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
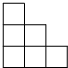 一些完全相同的小正方体搭成一个几何体,这个几何体从正面和左面看所得的平面图形均为如图,小正方体的块数最多有( )
一些完全相同的小正方体搭成一个几何体,这个几何体从正面和左面看所得的平面图形均为如图,小正方体的块数最多有( )| A、11块 | B、12块 |
| C、13块 | D、14块 |
安徽省有682000名初中毕业生参加中考,按四舍五入保留两位有效数字,682000用科学记数法表示为( )
| A、0.69×106 |
| B、6.82×1 05 |
| C、0.68×106 |
| D、6.8×105 |
中国电信公司最近推出的无线市话小灵通的通话收费标准为:前3分钟(不足3分钟按3分钟)为0.2元;3分钟后每分钟收0.1元,则一次通话实际那为x分钟(x>3)与这次通话的费用y(元)之间的函数关系是( )
| A、y=0.2+0.1x |
| B、y=0.1x |
| C、y=-0.1+0.1x |
| D、y=0.5+0.1x |
 如图,AB是⊙O的直径,弦CD平分∠ACB,则∠3=
如图,AB是⊙O的直径,弦CD平分∠ACB,则∠3=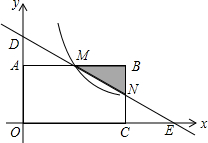 如图在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
如图在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.