题目内容
3.已知y=$\frac{2}{x}$,求(x+y)2-x(5y+x)-y2的值.分析 首先由y=$\frac{2}{x}$,得出xy=2,进一步利用完全平方公式和整式的乘法计算,进一步合并整体代入求得答案即可.
解答 解:∵y=$\frac{2}{x}$,
∴xy=2,
∵(x+y)2-x(5y+x)-y2
=x2+2xy+y2-5xy-x2-y2
=-3xy,
∴(x+y)2-x(5y+x)-y2=-6.
点评 此题考查整式的混合运算与化简求值,掌握计算方法,整体代入是解决问题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
18.甲、乙两名同学在参加体育中考前各作了5次投掷实心球的测试,甲所测的成绩分别为10.2m,9m,9.4m,8.2m,9.2m,乙所测得的成绩的平均数与甲相同且所测成绩的方差为0.72,那么( )
| A. | 甲、乙成绩一样稳定 | B. | 甲成绩更稳定 | ||
| C. | 乙成绩更稳定 | D. | 不能确定谁的成绩更稳定 |
8.在实数0,-$\sqrt{3}$,-$\frac{2}{3}$,|-2|中,最小的数是( )
| A. | -$\frac{2}{3}$ | B. | 0 | C. | -$\sqrt{3}$ | D. | |-2| |
15.甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数是9.2环,方差分别为S甲2=0.56,S乙2=0.60,S丙2=0.51,S丁2=0.58,则成绩最稳定的是( )
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
13.在一个袋子中装有除颜色外其它均相同的2个红球和3个白球,从中任意摸出一个球,摸到红球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
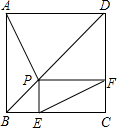 如图,点P为正方形ABCD对角线BD上一点,PE⊥BC于E,PF⊥DC于F.
如图,点P为正方形ABCD对角线BD上一点,PE⊥BC于E,PF⊥DC于F.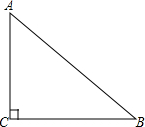 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.