题目内容
14.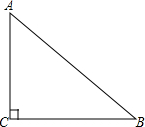 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.(1)按以下步骤作图并保留作图痕迹.
①以点A为圆心,以小于AC长为半径画弧,交AC于点E,交AB于点F;
②分别以点E,F为圆心,以大于$\frac{1}{2}$EF长为半径画弧,两弧在Rt△ABC的内部相交
于点M;
③画射线AM交BC于点D.
(2)求证:AD是∠BAC的平分线.
分析 (1)根据题目要求作出图形即可;
(2)连接EM、FM,然后证明△AEM≌△AFM,可得∠CAD=∠BAD,进而可得AD是∠BAC的平分线.
解答 (1)解:如图所示:
(2)证明:连接EM、FM,
根据作图可的AE=AF,EM=FM,
在△AEM和△AFM中,
$\left\{\begin{array}{l}{AE=AF}\\{AM=AM}\\{EM=FM}\end{array}\right.$,
∴△AEM≌△AFM(SSS),
∴∠CAD=∠BAD,
∴AD是∠BAC的平分线.
点评 此题主要考查了基本作图,以及全等三角形的判定和性质,关键是掌握证明两个三角形全等的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.2014年巴西世界杯在南美洲国家巴西境内12座城市中的12座球场内举行,本届世界杯的冠军将获得3500万美元的奖励,将3500万用科学记数法表示为( )
| A. | 3.5×106 | B. | 3.5×l07 | C. | 35×l06 | D. | 0.35×l08 |
5.在科学计算器上按顺序按3,8,×,1,5,+,3,2,=,最后屏幕上显示( )
| A. | 686 | B. | 602 | C. | 582 | D. | 502 |
9. 关于x的不等式$x-3>\frac{3x+a}{2}$的解集在数轴上表示如图所示,则a的值是( )
关于x的不等式$x-3>\frac{3x+a}{2}$的解集在数轴上表示如图所示,则a的值是( )
 关于x的不等式$x-3>\frac{3x+a}{2}$的解集在数轴上表示如图所示,则a的值是( )
关于x的不等式$x-3>\frac{3x+a}{2}$的解集在数轴上表示如图所示,则a的值是( )| A. | -6 | B. | -12 | C. | 6 | D. | 12 |
 已知点A、B和直线l,求作:点P,使点P在直线l上,且PA=PB.
已知点A、B和直线l,求作:点P,使点P在直线l上,且PA=PB.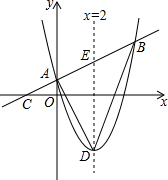 如图,对称轴为直线x=2的抛物线y=x2+mx+1的顶点为D,与y轴相交于点A,过点A作AD的垂线交x轴于点C,交抛物线的对称轴于点E,且与抛物线的另一个交点为B.
如图,对称轴为直线x=2的抛物线y=x2+mx+1的顶点为D,与y轴相交于点A,过点A作AD的垂线交x轴于点C,交抛物线的对称轴于点E,且与抛物线的另一个交点为B.