题目内容
12.在等腰三角形中,已知腰为5,底为8,则底边上的高为3.分析 根据等腰三角形的性质可以得出BD=CD=$\frac{1}{2}$BC,再由勾股定理即可得出结论.
解答 解:依照题意画出图形,如图所示.
∵AB=AC,AD⊥BC,
∴BD=CD=$\frac{1}{2}$BC=4,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=3.
故答案为:3.
点评 本题考查了等腰三角形的性质以及勾股定理,解题的关键是利用勾股定理求出线段AD的长.本题属于基础题,难度不大,解决该题型题目时,根据等腰三角形的性质求出底边的一半,再利用勾股定理求出底边上的高线长度是关键.

练习册系列答案
相关题目
10.反比例函数y=-$\frac{3}{x}$的图象上有(-2,y1);(-3,y2)两点,则y1与y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不确定 |
11.小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为80分、85分、90分,若依次按照2:3:5的比例确定成绩,则小王的成绩是( )
| A. | 255分 | B. | 84.5分 | C. | 85.5分 | D. | 86.5分 |
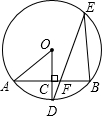 如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O上.
如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O上.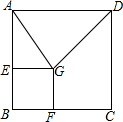 如图,正方形ABCD的边长是2,点E、F分别是AB、BC边上的动点(不与点A、B、C重合),且BE=BF,EG⊥AB,FG⊥BC,EG与FG相交于点G,当△ADG为等腰三角形时,BE的长为1或2-$\sqrt{2}$.
如图,正方形ABCD的边长是2,点E、F分别是AB、BC边上的动点(不与点A、B、C重合),且BE=BF,EG⊥AB,FG⊥BC,EG与FG相交于点G,当△ADG为等腰三角形时,BE的长为1或2-$\sqrt{2}$. 如图,点C在线段AE上,BC∥DE,AC=DE,BC=CE.求证:∠A=∠D.
如图,点C在线段AE上,BC∥DE,AC=DE,BC=CE.求证:∠A=∠D. 如图,在?ABCD中,AE⊥BC,垂足为E,AB=5,BC=8,sinB=$\frac{4}{5}$,那么S△CDE=10.
如图,在?ABCD中,AE⊥BC,垂足为E,AB=5,BC=8,sinB=$\frac{4}{5}$,那么S△CDE=10.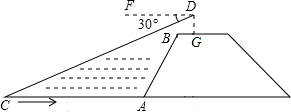 如图,小华站在河岸上的G点,看见河里有一小船沿垂直于岸边的方向划过来.此时测得小船C的俯角是∠FDC=30°.若小华的眼睛与地面的距离是$\sqrt{3}$米,BG=1.5米,BG平行于AC所在的直线,迎水坡i=4:3,坡长AB=10米,点A、B、C、D、F、G在同一平面内,则此时小船C到岸边的距离CA的长是多少?(结果保留根号)
如图,小华站在河岸上的G点,看见河里有一小船沿垂直于岸边的方向划过来.此时测得小船C的俯角是∠FDC=30°.若小华的眼睛与地面的距离是$\sqrt{3}$米,BG=1.5米,BG平行于AC所在的直线,迎水坡i=4:3,坡长AB=10米,点A、B、C、D、F、G在同一平面内,则此时小船C到岸边的距离CA的长是多少?(结果保留根号)