题目内容
1. 如图,在?ABCD中,AE⊥BC,垂足为E,AB=5,BC=8,sinB=$\frac{4}{5}$,那么S△CDE=10.
如图,在?ABCD中,AE⊥BC,垂足为E,AB=5,BC=8,sinB=$\frac{4}{5}$,那么S△CDE=10.
分析 首先由已知条件和勾股定理得出AE=4,BE=3,求出CE=5,由三角形的面积公式即可得出S△CDE.
解答 解:在△ABE中,AE⊥BC,AB=5,sinB=$\frac{AE}{AB}$=$\frac{4}{5}$,
∴AE=4,
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=3,
∴CE=BC-BE=8-3=5,
∴S△CDE=$\frac{1}{2}$CE•AE=$\frac{1}{2}$×5×4=10;
故答案为:10.
点评 本题考查了解直角三角形的运用、勾股定理的运用、平行四边形的性质;由三角函数和勾股定理求出AE和BE是解决问题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
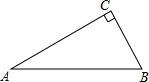 如图,△ABC中,∠C=90°,∠A=30°.
如图,△ABC中,∠C=90°,∠A=30°.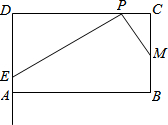 如图,在矩形ABCD中,AB=m,BC=4,点M为边BC的中点,点P为边CD上的动点(点P异于C,D两点).连接PM,过点P作PM的垂线与射线DA相交于点E(如图).
如图,在矩形ABCD中,AB=m,BC=4,点M为边BC的中点,点P为边CD上的动点(点P异于C,D两点).连接PM,过点P作PM的垂线与射线DA相交于点E(如图).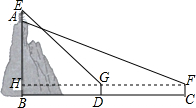 数学实践活动小组实地测量山峰与山下广场的相对高度AB,器测量步骤如下:
数学实践活动小组实地测量山峰与山下广场的相对高度AB,器测量步骤如下: