题目内容
17.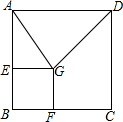 如图,正方形ABCD的边长是2,点E、F分别是AB、BC边上的动点(不与点A、B、C重合),且BE=BF,EG⊥AB,FG⊥BC,EG与FG相交于点G,当△ADG为等腰三角形时,BE的长为1或2-$\sqrt{2}$.
如图,正方形ABCD的边长是2,点E、F分别是AB、BC边上的动点(不与点A、B、C重合),且BE=BF,EG⊥AB,FG⊥BC,EG与FG相交于点G,当△ADG为等腰三角形时,BE的长为1或2-$\sqrt{2}$.
分析 首先判断点G在对角线上,分两种情形讨论①DA=DG,②GA=GD.求出BG,再根据BE=$\frac{\sqrt{2}}{2}$BG即可解决问题.
解答 解:∵四边形ABCD是正方形,四边形BEGF是正方形,
∴AB=BC=CD=AD=2,∠EBG=∠ABD=45°,
∴B、G、D共线,BD=2$\sqrt{2}$,
当DA=DG时,BG=2$\sqrt{2}$-2,
∴BE=$\frac{\sqrt{2}}{2}$•BG=2-$\sqrt{2}$,
当GA=DG时,G是BD中点,
∴BG=$\sqrt{2}$,
∴BE=$\frac{\sqrt{2}}{2}$BG=1,
故答案为1或2-$\sqrt{2}$
点评 本题考查正方形的性质、等腰三角形的性质等知识,解题的关键是判断点G的位置,注意考虑问题要全面,学会分类讨论,属于中考常考题型.

练习册系列答案
相关题目
15.若分式$\frac{{{x^2}-4}}{(x+1)(x-2)}$的值为0,则x的值为( )
| A. | 2 | B. | -2 | C. | 2或-2 | D. | 2或-1 |
16.使$\sqrt{3x-1}$有意义的x的取值范围是( )
| A. | x>-$\frac{1}{3}$ | B. | x>$\frac{1}{3}$ | C. | x≥$\frac{1}{3}$ | D. | x≥-$\frac{1}{3}$ |
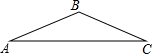 如图,一座厂房屋顶人字架的跨度AC=12m,上弦AB=BC,∠BAC=25°.若用科学计算器求上弦AB的长,则下列按键顺序正确的是( )
如图,一座厂房屋顶人字架的跨度AC=12m,上弦AB=BC,∠BAC=25°.若用科学计算器求上弦AB的长,则下列按键顺序正确的是( )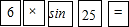



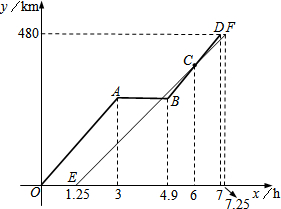 “十•一”长假,小王与小叶相约分别驾车从南京出发,沿同一路线驶往距南京480km的甲地旅游.小王由于有事临时耽搁,比小叶迟出发1.25小时.而小叶的汽车中途发生故障,等排除故障后,立即加速赶往甲地.若从小叶出发开始计时,图中的折线O-A-B-D、线段EF分别表示小叶、小王两人与南京的距离y1(km)、y2(km)与时间x(h)之间的函数关系.
“十•一”长假,小王与小叶相约分别驾车从南京出发,沿同一路线驶往距南京480km的甲地旅游.小王由于有事临时耽搁,比小叶迟出发1.25小时.而小叶的汽车中途发生故障,等排除故障后,立即加速赶往甲地.若从小叶出发开始计时,图中的折线O-A-B-D、线段EF分别表示小叶、小王两人与南京的距离y1(km)、y2(km)与时间x(h)之间的函数关系. 如图,△ABC中,∠C=90°,∠A=30°.
如图,△ABC中,∠C=90°,∠A=30°.