题目内容
4．
如图，点C在线段AE上，BC∥DE，AC=DE，BC=CE．求证：∠A=∠D．
分析 利用SAS可证△ABC≌△CDE，从而可得∠A=∠D．
解答 证明：∵BC∥DE，
∴∠BCA=∠CED，
在△ABC与△CED中，
$\left\{\begin{array}{l}{AC=DE}\\{∠BCA=∠CED}\\{BC=CE}\end{array}\right.$，
∴△ABC≌△CED（SAS），
∴∠A=∠D
点评 本题考查了全等三角形的判定和性质，解题的关键是证明对应角∠D=∠A．
练习册系列答案
相关题目
2．小亮所在的校篮球队12名队员的平均身高为1.82米，小亮的身高是1.84米，则下列说法正确的是（ ）
| A． | 篮球队员身高的中位数一定大于1.82米 | |
| B． | 篮球队员身高的众数一定小于1.82米 | |
| C． | 篮球队中比小亮高的队员不会超过5人 | |
| D． | 篮球队员身高的中位数与众数有可能相同 |
3．
如图，在Rt△ABC中，∠ABC=90°，∠B=60°，BC=2，△A′B′C是由△ABC绕C点顺时针旋转得到，其中点A′与点A是对应点，点B′与点B是对应点，连接AB′，且A，B′，A′在同一条直线上，则AA′的长为（ ）
如图，在Rt△ABC中，∠ABC=90°，∠B=60°，BC=2，△A′B′C是由△ABC绕C点顺时针旋转得到，其中点A′与点A是对应点，点B′与点B是对应点，连接AB′，且A，B′，A′在同一条直线上，则AA′的长为（ ）| A． | 6 | B． | 4$\sqrt{3}$ | C． | 3$\sqrt{3}$ | D． | 3 |
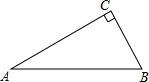如图，△ABC中，∠C=90°，∠A=30°．
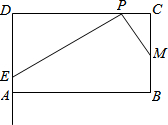如图，在矩形ABCD中，AB=m，BC=4，点M为边BC的中点，点P为边CD上的动点（点P异于C，D两点）．连接PM，过点P作PM的垂线与射线DA相交于点E（如图）．
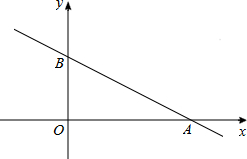如图，在以点O为原点的直角坐标系中，一次函数y=-$\frac{1}{2}$x+1的图象与x轴交于A，与y轴交于点B，求：