题目内容
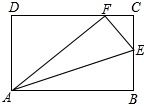 如图,矩形ABCD中,E是BC上一点,将矩形沿AE翻折后,点B恰好与CD边上的点F重合.已知AB=5,AD=3.
如图,矩形ABCD中,E是BC上一点,将矩形沿AE翻折后,点B恰好与CD边上的点F重合.已知AB=5,AD=3.(1)求BE;
(2)求tan∠EAF.
考点:翻折变换(折叠问题)
专题:
分析:(1)先根据勾股定理得到DF的长,在Rt△CEF中,CF=CD-DF=1,根据cos∠CFE=cos∠DAF,可得关于EF的方程,解得EF的长,即为BE的长;
(2)根据tan∠EAF=tan∠EAB,由正切的定义即可求解.
(2)根据tan∠EAF=tan∠EAB,由正切的定义即可求解.
解答:解:(1)(方法一)依题意,AF=AB=5,DF=
=4,
在Rt△CEF中,CF=CD-DF=1,∠CFE=∠DAF=90°-∠AFD,cos∠CFE=cos∠DAF,
所以
=
解得EF=
=
,所以BE=EF=
…(7分)
(方法二)依题意,AF=AB=5,DF=
=4
设BE=x,
在Rt△CEF中,CF=CD-DF=1,EF=BE=x,CE=3-x
x2=12+(3-x)2,
解得BE=x=
;
(2)tan∠EAF=tan∠EAB=
=
.
| AF2-AD2 |
在Rt△CEF中,CF=CD-DF=1,∠CFE=∠DAF=90°-∠AFD,cos∠CFE=cos∠DAF,
所以
| CF |
| EF |
| AD |
| AF |
解得EF=
| CF×AF |
| AD |
| 5 |
| 3 |
| 5 |
| 3 |
(方法二)依题意,AF=AB=5,DF=
| AF2-AD2 |
设BE=x,
在Rt△CEF中,CF=CD-DF=1,EF=BE=x,CE=3-x
x2=12+(3-x)2,
解得BE=x=
| 5 |
| 3 |
(2)tan∠EAF=tan∠EAB=
| BE |
| AB |
| 1 |
| 3 |
点评:此题考查了折叠的性质、矩形的性质以及三角函数等知识.此题难度适中,注意掌握折叠前后图形的对应关系,注意数形结合思想与转化思想的应用.

练习册系列答案
相关题目

 如图,已知⊙O的直径AB=16,点C是⊙O的一点,且
如图,已知⊙O的直径AB=16,点C是⊙O的一点,且
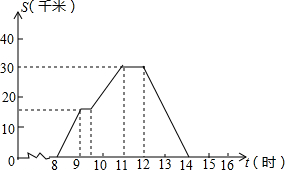 一天上午8:00时,小华去县城购物,到下午14:00时返回家,设他离家的距离为s千米,结合图象回答:
一天上午8:00时,小华去县城购物,到下午14:00时返回家,设他离家的距离为s千米,结合图象回答: 托盘秤是日常生活中一种常见的称重仪器(如图).小华同学发现刻度盘上的顺时针指针偏离0刻度的角度与托盘上物体重量符合一次函数关系,并制作了下表.
托盘秤是日常生活中一种常见的称重仪器(如图).小华同学发现刻度盘上的顺时针指针偏离0刻度的角度与托盘上物体重量符合一次函数关系,并制作了下表.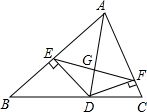 已知:如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,EF交AD于点G.
已知:如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,EF交AD于点G.