Question

已知：如图1，△MNQ中，MQ≠NQ．

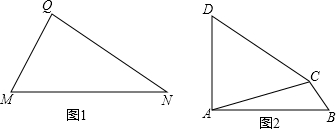
（1）请你以MN为一边，在MN的同侧构造一个与△MNQ全等的三角形，画出图形，并简要说明构造的方法；
（2）参考（1）中构造全等三角形的方法解决下面问题：
     如图2，在四边形ABCD中，∠ACB+∠CAD=180°，∠B=∠D．求证：CD=AB．

Answer 1

考点：全等三角形的判定与性质

专题：

分析：（1）以点N为圆心，以MQ长度为半径画弧，以点M为圆心，以NQ长度为半径画弧，两弧交于一点F，则△MNF为所画三角形．
（2）延长DA至E，使得AE=CB，连结CE．证明△EAC≌△BCA，得：∠B =∠E，AB=CE，根据等量代换可以求得答案．

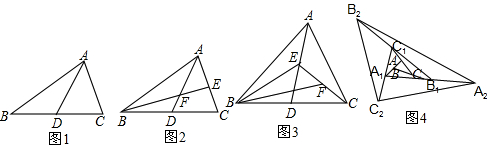
解答：解：（1）如图1，以N 为圆心，以MQ 为半径画圆弧；以M 为圆心，以NQ 为半径画圆弧；两圆弧的交点即为所求．

主要根据“SSS”判定三角形的全等．
（2）如图3，

延长DA至E，使得AE=CB，连结CE．．
∵∠ACB +∠DAC =180°，∠DAC +∠EAC =180°
∴∠ACB=∠EAC
在△EAC和△BAC中，

AE=CB ∠EAC=∠BCA AC=CA

∴△EAC≌△BCA （SAS）
∴∠B=∠E，AB=CE
∵∠B=∠D，
∴∠D=∠E
∴CD=CE
∴CD=AB．

点评：本题考查了尺规作图方法以及三角形全等的判定方法，解答本题的关键是要学会辅助线的作法，给解题创造更便捷的方法．