题目内容
6.在数学学习中整体思想与转化思想是我们常用到的数学思想.如图(1)中,求∠A+∠B+∠C+∠D+∠E的度数等于多少时,我们可以连接CD,利用三角形的内角和则有∠B+∠E=∠ECD+∠BDC,这样∠A、∠B、∠C、∠D、∠E的和就转化到同一个△ACD中,即∠A+∠B+∠C+∠D+∠E=180°.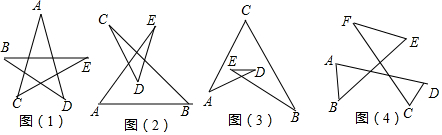
尝试练习:
图(2)中∠A+∠B+∠C+∠D+∠E的度数等于180°.
图(3)中∠A+∠B+∠C+∠D+∠E的度数等于180°.
图(4)中∠A+∠B+∠C+∠D+∠E+∠F的度数等于360°.
分析 仿照材料、根据三角形内角和定理计算即可.
解答  解:如图(2),连接CE,
解:如图(2),连接CE,
则有∠A+∠B=∠AEC+∠BCE,
∴∠A+∠B+∠DCB+∠D+∠DEA=180°;
同理,图(3)中∠A+∠B+∠C+∠D+∠E=180°;
图(4)中∠A+∠B+∠C+∠D+∠E+∠F=360°.
故答案为:180°;180°;360°.
点评 本题考查的是三角形内角和定理,掌握三角形内角和等于180°是解题的关键.

练习册系列答案
相关题目
16.若a-b=1,则2-2a+2b的值是( )
| A. | 0 | B. | -1 | C. | -2 | D. | 4 |
14.阅读表:
解答下列问题:
(1)根据表中规律猜测线段总数N与线段上的点数n(包括线段两个端点)有什么关系?
(2)根据上述关系解决如下实际问题:有一辆客车往返于A,B两地,中途停靠三个站点,如果任意两站间的票价都不同,问:①有10种不同的票价?②要准备20种车票?(直接写答案)
| 线段AB上的点数n(包括A,B两点) | 图例 | 线段总条数N |
| 3 |  | 3=2+1 |
| 4 |  | 6=3+2+1 |
| 5 |  | 10=4+3+2+1 |
| 6 |  | 15=5+4+3+2+1 |
(1)根据表中规律猜测线段总数N与线段上的点数n(包括线段两个端点)有什么关系?
(2)根据上述关系解决如下实际问题:有一辆客车往返于A,B两地,中途停靠三个站点,如果任意两站间的票价都不同,问:①有10种不同的票价?②要准备20种车票?(直接写答案)
1.股民周思源上周五在股市以收盘价(收市时的价格)买进某公司股票1000股,每股25元,周六、周日股市不交易,在接下来的一周交易日内,周思源记下该股票每日收盘价格相比前一天的涨跌情况:(单位:元)
根据上表回答问题:
(1)星期二收盘时,该股票每股多少元?
(2)这一周内该股票收盘时的最高价,最低价分别是多少?
(3)已知买入股票与卖出股票均需支付成交总金额的5‰(千分之五)的交易费.若小王在本周五以收盘价将全部股票卖出,他的收益情况如何?
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌(元) | +2 | -1.4 | +0.9 | -1.8 | +0.5 |
(1)星期二收盘时,该股票每股多少元?
(2)这一周内该股票收盘时的最高价,最低价分别是多少?
(3)已知买入股票与卖出股票均需支付成交总金额的5‰(千分之五)的交易费.若小王在本周五以收盘价将全部股票卖出,他的收益情况如何?
18.已知函数y=-$\frac{1}{x}$,当x≥-1时,y的取值范围是( )
| A. | y≥1 | B. | y≤1 | C. | y≥1或y<0 | D. | y≤1或y>0 |

 如图是某种电子产品的主板示意图,每一个转角处都是直角.已知AB=75mm,BC=90mm,则该主板的周长是330mm.
如图是某种电子产品的主板示意图,每一个转角处都是直角.已知AB=75mm,BC=90mm,则该主板的周长是330mm.