已知函数y=-$\frac{1}{x}$.当x≥-1时.y的取值范围是( )A．y≥1B．y≤1C．y≥1或y＜0D．y≤1或y＞0 题目和参考答案——青夏教育精英家教网—

题目内容

18．已知函数y=-$\frac{1}{x}$，当x≥-1时，y的取值范围是（　　）

A．

y≥1

B．

y≤1

C．

y≥1或y＜0

D．

y≤1或y＞0

分析首先根据k值确定反比例函数的增减性，然后根据自变量的取值确定反比例函数的函数值的取值范围．

解答解：∵函数y=-$\frac{1}{x}$中k=-1＜0，
∴在每个象限内y随着x的增大而增大，
∵当x=-1时，y=1，
∴当-1≤x＜0时，y≥1，
当x＞0时，y＜0，
即y≥1或y＜0，
故选C．

点评本题考查了反比例函数的性质，首先根据反比例函数的比例系数确定其增减性，然后确定函数值的取值范围，本题也可利用函数的图象解题．

练习册系列答案

	A．	289（1-2x）=256		B．	256（1+x）²=289
	C．	289（1-x）²=256		D．	289-289（1-x）-289（1-x）²=256

9．下列运用等式的性质，变形不正确的是（　　）

若x=y，则$\frac{x}{a}$=$\frac{y}{a}$

6．在数学学习中整体思想与转化思想是我们常用到的数学思想．如图（1）中，求∠A+∠B+∠C+∠D+∠E的度数等于多少时，我们可以连接CD，利用三角形的内角和则有∠B+∠E=∠ECD+∠BDC，这样∠A、∠B、∠C、∠D、∠E的和就转化到同一个△ACD中，即∠A+∠B+∠C+∠D+∠E=180°．

尝试练习：
图（2）中∠A+∠B+∠C+∠D+∠E的度数等于180°．
图（3）中∠A+∠B+∠C+∠D+∠E的度数等于180°．
图（4）中∠A+∠B+∠C+∠D+∠E+∠F的度数等于360°．

13．若xy=1，则化简（x-$\frac{1}{x}$）（y+$\frac{1}{y}$）结果为（　　）

2x²

2y²

y²-x²

x²-y²

3．

如图，在△ABC中，AB=AC，∠BAC=90°，D，E分别在边BC，AC上，∠ADE=45°．
求证：△ABD∽△DCE．

10．

如图，把一张矩形的纸片沿图中的虚线裁成三张大小相同的小矩形纸片．若得到的小矩形纸片与原来大矩形纸片相似，则大矩形纸片的长与宽的比值为$\sqrt{3}$．

7．将方程3x²+1=6x化为一元二次方程的一般形式，其中二次项系数为3，则一次项系数、常数项分别是（　　）

13．

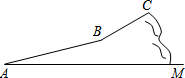今年“五一”假期，某数学活动小组组织一次登山活动．他们从山脚下A点出发沿斜坡AB到达B点，再从B点沿斜坡BC到达山顶C点，路线如图所示．斜坡AB的长为1040米，斜坡BC的长为400米，在C点测得B点的俯角为30°，．已知A点海拔191米，C点海拔791米．
（1）求B点的海拔；
（2）求斜坡AB的坡度．

试题分类