题目内容
18.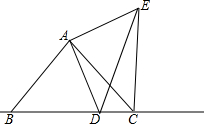 如图,△ABC为等腰直角三角形,AB=AC,∠BAC=90°
如图,△ABC为等腰直角三角形,AB=AC,∠BAC=90°(1)小刚拿了一个等腰直角三角板,AD=AE,把直角顶点与点A重合,旋转三角板到如图的位置,点D在BC上(点D不与B,C重合),并连接EC,他猜想,图中是否有全等三角形呢?请你帮他找出一对全等三角形,并写出思考过程
(2)在(1)的条件下,∠AEC=∠ACB+∠DAC是否成立?请说明理由.
分析 (1)先由等腰直角三角形的性证出∠BAC=∠DAE,再由SAS即可证出△ABD≌△ACE;
(2)由△ABD≌△ACE,得出∠ADB=∠AEC,再由外角的性质得出∠ADB=∠ACD+∠DAC,即可得出结论.
解答 解:(1)△ABD≌△ACE;理由如下:
∵∠BAC=90°,∠DAE=90°,
∴∠BAC=∠DAE.
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,$\left\{\begin{array}{l}{AB=AC}&{\;}\\{∠BAD=∠CAE}&{\;}\\{AD=AE}&{\;}\end{array}\right.$,
∴△ABD≌△ACE(SAS);
(2)成立;理由如下:
∵△ABD≌△ACE,
∴∠ADB=∠AEC,
∵∠ADB=∠ACD+∠DAC,
∴∠AEC=∠ACB+∠DAC.
点评 本题考查了等腰直角三角形的性质、全等三角形的判定与性质;熟练掌握等腰直角三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
13. 我县某校通过初评决定最后从甲、乙、丙三个班中推荐一个班为校先进班集体,下表是这三个班的五项素质考核表:五项成绩素质考评得分表(单位:分)
我县某校通过初评决定最后从甲、乙、丙三个班中推荐一个班为校先进班集体,下表是这三个班的五项素质考核表:五项成绩素质考评得分表(单位:分)
根据统计表中的信息下列问题:
(1)请你补全五项成绩考评分析表中的数据;
五项成绩考评分析表(单位:分)
(2)参照上表中的数据,你认为应该推荐哪个班为校先进班级?并说明理由;
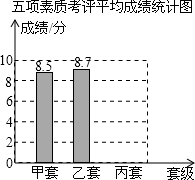
(3)如果学校把行为规范、学习成绩、校运动会、艺术获奖、劳动卫生五项考评成绩按3:2:1:1:3的权重确定,林老师根据这个总评成绩.绘制了一幅不完整的条形统计图,请将这个统计图补充完整,依照这个成绩,你应推荐哪个班为校先进班集体?
 我县某校通过初评决定最后从甲、乙、丙三个班中推荐一个班为校先进班集体,下表是这三个班的五项素质考核表:五项成绩素质考评得分表(单位:分)
我县某校通过初评决定最后从甲、乙、丙三个班中推荐一个班为校先进班集体,下表是这三个班的五项素质考核表:五项成绩素质考评得分表(单位:分)| 班级 | 行为规范 | 学习成绩 | 校运动会 | 艺术获奖 | 劳动卫生 |
| 甲 | 10 | 10 | 7 | 10 | 6 |
| 乙 | 10 | 8 | 8 | 9 | 8 |
| 丙 | 9 | 10 | 9 | 6 | 9 |
(1)请你补全五项成绩考评分析表中的数据;
五项成绩考评分析表(单位:分)
| 班级 | 平均数 | 众数 | 中位数 |
| 甲 | 8.6 | 10 | 10 |
| 乙 | 8.6 | 8 | 8 |
| 丙 | 8.6 | 9 | 9 |
(3)如果学校把行为规范、学习成绩、校运动会、艺术获奖、劳动卫生五项考评成绩按3:2:1:1:3的权重确定,林老师根据这个总评成绩.绘制了一幅不完整的条形统计图,请将这个统计图补充完整,依照这个成绩,你应推荐哪个班为校先进班集体?
10.关于x的方程mx2-$\sqrt{5-m}$x-1=0有两个实数解,则m的取值范围是( )
| A. | m≥-$\frac{5}{3}$ | B. | 0<m≤5 | C. | -$\frac{5}{3}$≤m≤5且m≠0 | D. | 0<m≤5且m≠0 |
7.已知x2-x-1=0,则x3-2x+1的值为( )
| A. | $\sqrt{5}$-1 | B. | 2 | C. | -1 | D. | -2 |
8.下列几何图形中,既是中心对称图形又是轴对称图形的个数是( )

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
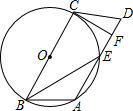 如图,已知在四边形ABCD中,∠ABC=∠D,过A、B、C三点作⊙O交AD于点E,C是$\widehat{AEB}$的中点,CF⊥AD于点F.
如图,已知在四边形ABCD中,∠ABC=∠D,过A、B、C三点作⊙O交AD于点E,C是$\widehat{AEB}$的中点,CF⊥AD于点F.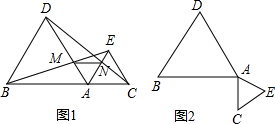
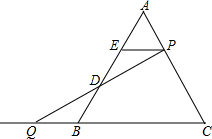 如图,△ABC是等边三角形,P是AC边上任意一点(与A、C两点不重合),Q是CB延长线上一点,且始终满足条件BQ=AP,过P作PE∥BC交AB于点E,连接PQ交AB于D.
如图,△ABC是等边三角形,P是AC边上任意一点(与A、C两点不重合),Q是CB延长线上一点,且始终满足条件BQ=AP,过P作PE∥BC交AB于点E,连接PQ交AB于D.