题目内容
16.解下列不等式:(1)|$\frac{3x-1}{2}$|≤4;
(2)(3x-6)(2x-1)>0.
分析 (1)根据绝对值的意义得出两个不等式,求出每个不等式的解集集;
(2)根据乘法法则得出两个不等式组,求出不等式组的解集即可.
解答 解:(1)原不等式化为两种情况:①当$\frac{3x-1}{2}$≥0,即x≥$\frac{1}{3}$时,$\frac{3x-1}{2}$≤4,
3x-1≤8,
3x≤9,
x≤3,
所以原不等式的解集为$\frac{1}{3}$≤x≤3;
②当$\frac{3x-1}{2}$<0,即x$<\frac{1}{3}$时,-$\frac{3x-1}{2}$≤4,
-3x+1≤8,
-3x≤7,
x≥-$\frac{7}{3}$,
所以原不等式的解集为-$\frac{7}{3}$≤x<$\frac{1}{3}$;
(2)(3x-6)(2x-1)>0
可化为:①$\left\{\begin{array}{l}{3x-6>0}\\{2x-1>0}\end{array}\right.$或②$\left\{\begin{array}{l}{3x-6<0}\\{2x-1<0}\end{array}\right.$,
不等式组①的解及时x>2,不等式组②的解集是x<$\frac{1}{2}$,
所以原不等式的解集为x>2或x$<\frac{1}{2}$.
点评 本题考查了解一元一次不等式,解一元一次不等式组,绝对值的应用,解此题的关键是能根据题意得出两个一元一次不等式或一元一次不等式组,难度适中.

练习册系列答案
相关题目
6.如图,在平面直角坐标系xOy中,点A(1,0),B(2,0),正六边形ABCDEF沿x轴正方向无滑动滚动,保持上述运动过程,经过(2014,$\sqrt{3}$)的正六边形的顶点是( )


| A. | C或E | B. | B或D | C. | A或E | D. | B或F |
1.若函数y=(m-2)x的图象经过第二、四象限,则m的取值范围是( )
| A. | m>2 | B. | m<2 | C. | m≥2 | D. | m≤2 |
7.已知x2-x-1=0,则x3-2x+1的值为( )
| A. | $\sqrt{5}$-1 | B. | 2 | C. | -1 | D. | -2 |
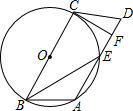 如图,已知在四边形ABCD中,∠ABC=∠D,过A、B、C三点作⊙O交AD于点E,C是$\widehat{AEB}$的中点,CF⊥AD于点F.
如图,已知在四边形ABCD中,∠ABC=∠D,过A、B、C三点作⊙O交AD于点E,C是$\widehat{AEB}$的中点,CF⊥AD于点F.