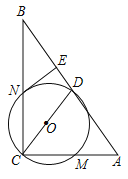Question

【题目】如图，是的直径，点为上一点，和过点的切线互相垂直，垂足为，交于点，直线交的延长线于点，连接，，．

[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/22/2490290299265024/2493010512216064/STEM/6108b9d591da4e268d6d47ef4c154d16.png]

（1）求证：平分；

（2）探究线段，之间的数量关系，并说明理由；

（3）若，求的面积．

Answer 1

【答案】（1）见解析；（2），见解析；（3）5

【解析】

（1）连接，根据切线的性质可得，然后根据平行线的判定可得，从而证出，根据等边对等角可得，从而证出，即可证出结论；

（2）根据直径所对的圆周角是直角可得，然后根据相似三角形的判定定理证出，列出比例式即可得出结论；

（3）过点作于点，根据相似三角形的判定定理可得，列出比例式即可求出OC，再根据，可得，最后根据勾股定理即可求出AC、BC，从而求出结论．

解：（1）证明：连接，

[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/22/2490290299265024/2493010512216064/EXPLANATION/c5818ff65a8a4699839c8defaae65c25.png]

∵是的切线，

∴，

∵，

∴，

∴，

∵，

∴，

∴，

∴平分；

（2）线段，之间的数量关系为：．

理由：∵是的直径，

∴，

∴，

∵，

∴，

∵，

∴，

∵，

∴，

∴，

∴

∵，

∴，

∴，

∴

（3）过点作于点，

则，四边形是矩形，

∴，

∴

∵，

∴，

∴，

∵，，

∴，

∴

∴，

∴，

∵，

∴，

∴

在中，

∴

∴，

∴

∴

[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/22/2490290299265024/2493010512216064/EXPLANATION/091db14000a2430dbf23cdd5aaba7021.png]