题目内容
1.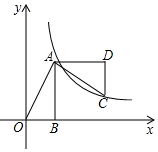 如图,已知在Rt△AOB中,点A(1,2),∠OBA=90°,OB在x轴上,将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k>0)上,则k的值为( )
如图,已知在Rt△AOB中,点A(1,2),∠OBA=90°,OB在x轴上,将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k>0)上,则k的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据A的坐标求AB、OB,根据旋转的性质求出AD和DC,求出C的坐标,即可得出答案.
解答 解:∵将△AOB绕点A逆时针旋转90°得到△ADC,
∴∠DAB=90°,∠D=∠ABO=90°,
∵∠ABO=90°,
∴AD∥OB,
∴DC⊥x轴,
∵A(1,2),
∴OB=1,OA=2,
∵∴AD=AB=2,DC=OB=1,
∴C点的坐标为(3,1),
把C的坐标代入y=$\frac{k}{x}$得:k=3,
故选C.
点评 本题考查了用待定系数法求反比例函数的解析式,坐标与图形变化-旋转等知识点,能根据旋转和A的坐标求出C的坐标是解此题的关键.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
9.与无理数$\sqrt{33}$-2最接近的整数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
10.某商场欲购进果汁饮料和碳酸饮料共50箱,两种饮料每箱进价和售价如下表所示:
设购进果汁饮料x箱(x为正整数),且所购进的两种饮料能全部卖出,获得的总利润为w元(注:总利润=总售价-总进价).
(1)求总利润w关于x的函数关系式;
(3)如果购进两种饮料的总费用不超过2000元,那么该商场如何进货才能获利最多?并求出最大利润.
| 饮料 | 果汁饮料 | 碳酸饮料 |
| 进价(元/箱) | 55 | 36 |
| 售价(元/箱) | 63 | 42 |
(1)求总利润w关于x的函数关系式;
(3)如果购进两种饮料的总费用不超过2000元,那么该商场如何进货才能获利最多?并求出最大利润.
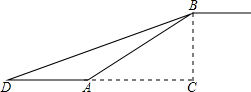 如图,在合肥地铁3号线某站通道的建设中,建设工人将坡长为20米(AB=20米)、坡角为20°30′(∠BAC=20°30′)的斜坡通道改造成坡角为12°30′(∠BDC=12°30′)的斜坡通道,使斜坡的起点从点A处向左平移至点D处,求改造后的斜坡通道BD的长.(结果精确到0.1米.参考数据:sin12°30′≈0.22,sin20°30′≈0.35,sin69°30′≈0.94).
如图,在合肥地铁3号线某站通道的建设中,建设工人将坡长为20米(AB=20米)、坡角为20°30′(∠BAC=20°30′)的斜坡通道改造成坡角为12°30′(∠BDC=12°30′)的斜坡通道,使斜坡的起点从点A处向左平移至点D处,求改造后的斜坡通道BD的长.(结果精确到0.1米.参考数据:sin12°30′≈0.22,sin20°30′≈0.35,sin69°30′≈0.94).
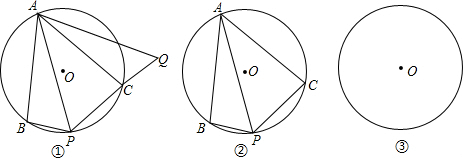
 如图,已知△ABC.点D,E分别是AB,AC的中点,若△ABC的面积等于24,则△ADE的面积等于6.
如图,已知△ABC.点D,E分别是AB,AC的中点,若△ABC的面积等于24,则△ADE的面积等于6.