题目内容
11.已知反比例函数y=$\frac{1}{x}$和一次函数y=-x+a-2(a为常数)(1)当a=0时,求反比例函数与一次函数的交点坐标.
(2)当反比例函数与一次函数有两个交点时,请确定a的范围.
分析 (1)根据a的值,可得一次函数的解析式,联立反比例函数与一次函数的解析式,可得方程组,解方程组,可得交点坐标;
(2)联立反比例函数与一次函数的解析式,可得方程组,根据反比例函数与一次函数有两个交点,可得方程组有2组解,根据一元二次方程的判别式,可得答案.
解答 解:(1)当a=0时,一次函数y=-x+a-2的解析式是y=-x-2,
联立反比例函数解析式、一次函数解析式,得$\left\{\begin{array}{l}{y=\frac{1}{x}}\\{y=-x-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$.
故当a=0时,反比例函数与一次函数的交点坐标是(-1,-1);
(2)存在实数a,使反比例函数与一次函数有两个交点,
联立反比例函数解析式、一次函数解析式,得$\left\{\begin{array}{l}{y=\frac{1}{x}}\\{y=-x+a-2}\end{array}\right.$.
由方程组有2组解,得
x2-(a-2)x+1=0有两个不相等的实数根.
△=[-(a-2)]2-4>0,
解得a<0或a>4.
故a的范围是a<0或a>4.
点评 本题考查了反比例函数与一次函数的交点问题,利用了方程组的解是函数图象的交点,判别式大于零一元二次方程有两个不相等的实数根.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
1.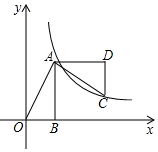 如图,已知在Rt△AOB中,点A(1,2),∠OBA=90°,OB在x轴上,将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k>0)上,则k的值为( )
如图,已知在Rt△AOB中,点A(1,2),∠OBA=90°,OB在x轴上,将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k>0)上,则k的值为( )
 如图,已知在Rt△AOB中,点A(1,2),∠OBA=90°,OB在x轴上,将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k>0)上,则k的值为( )
如图,已知在Rt△AOB中,点A(1,2),∠OBA=90°,OB在x轴上,将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k>0)上,则k的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.甲、乙两个仓库向A、B两地运送水泥,已知甲库可调出100吨水泥,乙库可调出80吨水泥,A地需70吨,B地需110吨水泥,两库到A,B两地的路程和费用如下表:(表中运费“元/吨•千米”表示每吨水泥运送1千米所需要人民币).
设甲库运往A地水泥x吨,总运费W元.
(1)写出w关于x的函数关系式,并求x为何值时总运费最小?
(2)如果要求运送的水泥数是10吨的整数倍,且运费不能超过38000元,则总共有几种运送方案?
| 路程(千米) | 运费(元/吨•千米) | |||
| 甲库 | 乙库 | 甲库 | 乙库 | |
| A地 | 20 | 15 | 12 | 12 |
| B地 | 25 | 20 | 10 | 8 |
(1)写出w关于x的函数关系式,并求x为何值时总运费最小?
(2)如果要求运送的水泥数是10吨的整数倍,且运费不能超过38000元,则总共有几种运送方案?
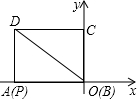 如图,在平面直角坐标系中,矩形ABCD的边AB,BC分别在x轴,y轴上,点D在第二象限,AB=8,BC=6,矩形ABCD沿OD方向以每秒1个单位长度的速度运动.同时点P从点A出发沿折线AD-DC以每秒1个单位长度向终点C运动,当点P到达点C时,矩形ABCD也停止运动,设点P的运动时间为r(s),△PDo的面积为S(平方单位),
如图,在平面直角坐标系中,矩形ABCD的边AB,BC分别在x轴,y轴上,点D在第二象限,AB=8,BC=6,矩形ABCD沿OD方向以每秒1个单位长度的速度运动.同时点P从点A出发沿折线AD-DC以每秒1个单位长度向终点C运动,当点P到达点C时,矩形ABCD也停止运动,设点P的运动时间为r(s),△PDo的面积为S(平方单位),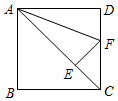 如图,已知E是正方形ABCD对角线AC上的一点,AE=AD,过点E作AC的垂线,交边CD于点F,∠FAD=22.5度.
如图,已知E是正方形ABCD对角线AC上的一点,AE=AD,过点E作AC的垂线,交边CD于点F,∠FAD=22.5度.