题目内容
求证:方程(
)2-y2=
无整数解.
| x+1 |
| 2 |
| 3 |
| 4 |
考点:因式分解的应用
专题:证明题
分析:首先将方程的左边因式分解,进而将该方程转化为二元一次方程组问题即可解决.
解答:解:∵方程(
)2-y2=
,
∴(
+y)(
-y)=
,
即(x+2y+1)(x-2y+1)=3,
若该方程有整数解,
则必有:
或
或
或
,
分别解上述方程组得:
或
或
或
,
这与已知该方程有整数解矛盾,
∴方程(
)2-y2=
无整数解.
| x+1 |
| 2 |
| 3 |
| 4 |
∴(
| x+1 |
| 2 |
| x+1 |
| 2 |
| 3 |
| 4 |
即(x+2y+1)(x-2y+1)=3,
若该方程有整数解,
则必有:
|
|
|
|
分别解上述方程组得:
|
|
|
|
这与已知该方程有整数解矛盾,
∴方程(
| x+1 |
| 2 |
| 3 |
| 4 |
点评:该命题以证明所给的方程无整数解为载体,着重考查了因式分解及其应用问题;解题的关键是准确运用因式分解法将所给方程的左边因式分解.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
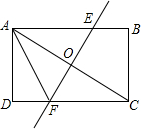 如图所示,将长方形ABCD沿直线EF对折,使顶点A与C重合在一起,折痕EF分别交CD、AB于点F,E交对角线AC相交于点O,已知AB=18cm,BC=12cm.
如图所示,将长方形ABCD沿直线EF对折,使顶点A与C重合在一起,折痕EF分别交CD、AB于点F,E交对角线AC相交于点O,已知AB=18cm,BC=12cm.
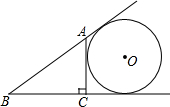 如图,AC⊥BC于点C,⊙O与直线AB、BC、CA都相切,若⊙O的半径等于1,BC=2,△ABC的周长是
如图,AC⊥BC于点C,⊙O与直线AB、BC、CA都相切,若⊙O的半径等于1,BC=2,△ABC的周长是