题目内容
已知函数y=(9k2-1)x2+2kx+3是关于x的二次函数,求不等式
≥
-1的解集.
| k-1 |
| 2 |
| 4k+1 |
| 3 |
考点:二次函数的定义,解一元一次不等式
专题:
分析:首先利用二次函数的定义得出k不能取的值,进而解不等式得出答案.
解答:解:∵函数y=(9k2-1)x2+2kx+3是关于x的二次函数,
∴9k2-1≠0,
解得:k≠±
,
≥
-1
3(k-1)≥2(4k+1)-6,
解得:k≤
,
故不等式
≥
-1的解集为:k≤
且k≠-
.
∴9k2-1≠0,
解得:k≠±
| 1 |
| 3 |
| k-1 |
| 2 |
| 4k+1 |
| 3 |
3(k-1)≥2(4k+1)-6,
解得:k≤
| 1 |
| 5 |
故不等式
| k-1 |
| 2 |
| 4k+1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 3 |
点评:此题主要考查了二次函数的定义以及解不等式,正确解不等式是解题关键.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
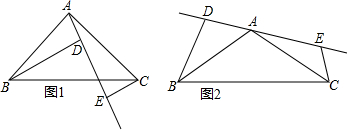
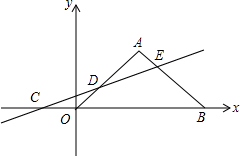 如图,△AOB是等腰三角形,且∠A=90°,点B坐标为(6,0),过点C(-3,0)作直线L交AO于点D,交AB于点E,且△ADE和△DCO的面积相等.
如图,△AOB是等腰三角形,且∠A=90°,点B坐标为(6,0),过点C(-3,0)作直线L交AO于点D,交AB于点E,且△ADE和△DCO的面积相等. 如图,直角梯形ABCD中,AD=3,AB=11,BC=6,AB⊥BC,动点P在线段AB上运动,如果满足△ADP和△BCP相似,计算此时线段AP的长度.
如图,直角梯形ABCD中,AD=3,AB=11,BC=6,AB⊥BC,动点P在线段AB上运动,如果满足△ADP和△BCP相似,计算此时线段AP的长度.