题目内容
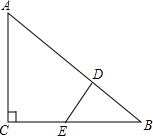 如图,△ABC中,∠C=90°,AC=BC,D是AB上一点,AD=AC,DE⊥AB,求证:BD=DE=CE.
如图,△ABC中,∠C=90°,AC=BC,D是AB上一点,AD=AC,DE⊥AB,求证:BD=DE=CE.考点:角平分线的性质,等腰直角三角形
专题:证明题
分析:先由△ABC中,∠C=90°,AC=BC,可得∠B=45°,又DE⊥AB,根据三角形内角和定理得出∠DEB=45°=∠B,由等角对等边得出BD=DE;再连接AE,易证Rt△ACE≌RT△ADE,可得CE=DE,即可解题.
解答:证明:∵△ABC中,∠C=90°,AC=BC,
∴∠B=∠A=45°,
又∵DE⊥AB,
∴∠DEB=45°=∠B,
∴BD=DE;
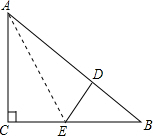 连接AE.
连接AE.
在Rt△ACE与RT△ADE中,
,
∴Rt△ACE≌RT△ADE(HL),
∴CE=DE,
∴BD=DE=CE.
∴∠B=∠A=45°,
又∵DE⊥AB,
∴∠DEB=45°=∠B,
∴BD=DE;
 连接AE.
连接AE.在Rt△ACE与RT△ADE中,
|
∴Rt△ACE≌RT△ADE(HL),
∴CE=DE,
∴BD=DE=CE.
点评:本题考查了全等三角形的判定与性质,等腰直角三角形的判定与性质,本题中求证Rt△ACE≌RT△ADE是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
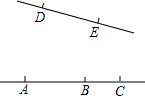 (1)如图,以点A、B、C、D、E中的任意3点为顶点的三角形共有
(1)如图,以点A、B、C、D、E中的任意3点为顶点的三角形共有 如图所示,△ABC中,AB=AC,∠C=30°,DA⊥AB于点A,若BC=6cm,求AB的长.
如图所示,△ABC中,AB=AC,∠C=30°,DA⊥AB于点A,若BC=6cm,求AB的长. 如图,在平行四边形ABCD中,点M是BC的中点,AM⊥BD,AM交BD于点P.且AM=9,BD=12.试求:
如图,在平行四边形ABCD中,点M是BC的中点,AM⊥BD,AM交BD于点P.且AM=9,BD=12.试求: 如图,∠1=48°,∠3=116°,∠4=64°,求∠2的度数.
如图,∠1=48°,∠3=116°,∠4=64°,求∠2的度数. 如图,在△ABC中,∠C=90°,sinA=
如图,在△ABC中,∠C=90°,sinA=