题目内容
 如图,在平行四边形ABCD中,点M是BC的中点,AM⊥BD,AM交BD于点P.且AM=9,BD=12.试求:
如图,在平行四边形ABCD中,点M是BC的中点,AM⊥BD,AM交BD于点P.且AM=9,BD=12.试求:(1)PB的长;
(2)AD的长.
考点:平行四边形的性质
专题:
分析:(1)由四边形ABCD是平行四边形,易证得△ADP∽△MBP,又由点M是BC的中点,AM=9,BD=12,然后根据相似三角形的对应边成比例,即可求得PB的长;
(2)由AM⊥BD,AP=6,DP=8,直接利用勾股定理求解即可求得答案.
(2)由AM⊥BD,AP=6,DP=8,直接利用勾股定理求解即可求得答案.
解答:解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△ADP∽△MBP,
∴AP:PM=AD:BM=DP:BP,
∵点M是BC的中点,
∴BM=
BC,
∴AP:PM=AD:BM=DP:BP=2:1,
∵AM=9,BD=12,
∴AP=6,PM=3,DP=8,PB=4;
(2)∵AM⊥BD,AP=6,DP=8,
∴AD=
=10.
∴AD∥BC,AD=BC,
∴△ADP∽△MBP,
∴AP:PM=AD:BM=DP:BP,
∵点M是BC的中点,
∴BM=
| 1 |
| 2 |
∴AP:PM=AD:BM=DP:BP=2:1,
∵AM=9,BD=12,
∴AP=6,PM=3,DP=8,PB=4;
(2)∵AM⊥BD,AP=6,DP=8,
∴AD=
| AP2+PD2 |
点评:此题考查了平行四边形的性质、相似三角形的判定与性质以及勾股定理.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
下列计算中,正确的是( )
| A、-0.12=0.2 |
| B、-|-2|2=4 |
| C、(-3)3=-6 |
| D、-(-1)2n+1=1(n表示自然数) |
 如图,在等腰△ABC中,AB=AC,AB=5cm,D为BC边上任意一点,DF∥AC,DE∥AB,点E,F分别在AB,AC上,求四边形AFDE的周长.
如图,在等腰△ABC中,AB=AC,AB=5cm,D为BC边上任意一点,DF∥AC,DE∥AB,点E,F分别在AB,AC上,求四边形AFDE的周长.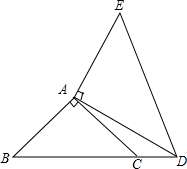 如图,△ABC是等腰直角三角形,在BC的延长线上取一点D,连接AD,以AD为腰作等腰直角△DAE,若BC=3,CD=1,求AD的长.
如图,△ABC是等腰直角三角形,在BC的延长线上取一点D,连接AD,以AD为腰作等腰直角△DAE,若BC=3,CD=1,求AD的长.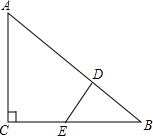 如图,△ABC中,∠C=90°,AC=BC,D是AB上一点,AD=AC,DE⊥AB,求证:BD=DE=CE.
如图,△ABC中,∠C=90°,AC=BC,D是AB上一点,AD=AC,DE⊥AB,求证:BD=DE=CE. 如图,以Rt△ABC的三边分别向外作三个正方形ACDE、BCNM、ABGH,其面积分别为S1,S2,S3,设Rt△ABC的两条直角边长为a,b,斜边长为c,请证明:S3=S1+S2.
如图,以Rt△ABC的三边分别向外作三个正方形ACDE、BCNM、ABGH,其面积分别为S1,S2,S3,设Rt△ABC的两条直角边长为a,b,斜边长为c,请证明:S3=S1+S2.